I use the nearest-neighbor interpolation operator (![]() )to map the data from an irregular mesh into a regular mesh.
Then, I use the PS-AMO operator to transform data
from non-zero crossline offsets (
)to map the data from an irregular mesh into a regular mesh.
Then, I use the PS-AMO operator to transform data
from non-zero crossline offsets (![]() ) to
zero crossline offset (hy=0), I refer to this operation
as an operator
) to
zero crossline offset (hy=0), I refer to this operation
as an operator ![]() which is a summation over hy. I allow some mixing
between hx by expanding our summation to form hx=a and hy=0
as following:
which is a summation over hy. I allow some mixing
between hx by expanding our summation to form hx=a and hy=0
as following:
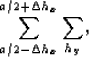 |
(12) |
I combine these two operators to estimate a 4-D model (![]() ) from
a 5-D irregular dataset (
) from
a 5-D irregular dataset (![]() ) through the objective function,
) through the objective function,
| |
(13) |
| (14) |
| |
(15) |
| |
(16) |
| |
(17) |
The solution of problem 13 is not
feasible on a single computer. The computational
requirements are onerous, but potentially manageable.
However, the memory requirements are not.
A full regularized 5-dimensional cube, that I create
after applying ![]() ,can easily reach tens of gigabytes. This size of data
makes it almost impossible to practically implement any
algorithm for 3-D prestack seismic data-processing on a single machine.
,can easily reach tens of gigabytes. This size of data
makes it almost impossible to practically implement any
algorithm for 3-D prestack seismic data-processing on a single machine.
() introduces an efficient python library for handling parallel jobs. The library makes it easy for the user to take an already existing serial code and transform it into a parallel code. The library handles distribution, collection, and node monitoring, commonly onerous tasks in parallel processing.
The main prerequisite to using the python library is to
build an efficient serial code,
and to describe
how the parallel job should be distributed on a cluster.
For this problem I chose to split along the hx axis.
I created a series of tasks, each assigned to produce a single
(![]() ) volume. Each task is passed
a range of hx's defined by equation 12. The resulting model
volumes are then recombined to form the regularized 4-D output space.
) volume. Each task is passed
a range of hx's defined by equation 12. The resulting model
volumes are then recombined to form the regularized 4-D output space.