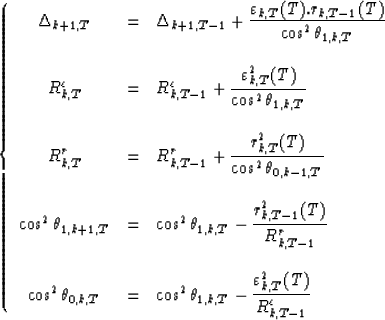Next: Exponential weighting
Up: THE LSL ALGORITHM
Previous: Recursions: order updating
In this part, the length of the filter is fixed, but we increase the length
of the processing window (from 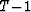 to T). Equation (3) tells
us how to compute
to T). Equation (3) tells
us how to compute 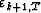 from
from 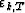 . But actually, we are
only interested in the
. But actually, we are
only interested in the 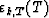 , and we don't want to compute, nor
store, the other values
, and we don't want to compute, nor
store, the other values 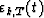 (
(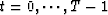 ) which form the
vector
) which form the
vector 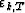 . It seems difficult then to compute
. It seems difficult then to compute 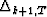 ,
,
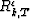 , or Rrk,T-1 !
, or Rrk,T-1 !
However, time-updating formulas also exist for these values, which only imply
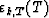 and rk,T-1(T). Their derivation is long, and I refer to
Lee et al. (1981) for an elegant proof. These authors use two other
intermediate variables, the angles
and rk,T-1(T). Their derivation is long, and I refer to
Lee et al. (1981) for an elegant proof. These authors use two other
intermediate variables, the angles 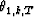 , and
, and 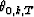 ;
especially,
;
especially, 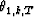 is defined as:
is defined as:
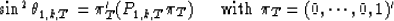
The recursions are now:
| 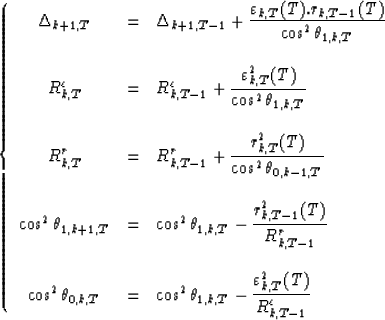 |
(4) |
In conclusion, the recursions (3), (4), and (5)
give us the entire set of recursions we need for the basic LSL algorithm. The
initialization procedures are precised in the sketch of the general LSL
algorithm I add at the end of the paper. The most important one is the
choice of an a priori value for the covariances, which will stabilize the
process by avoiding divisions by 0: it has more or less the stabilizing effect
of a prewhitening process on the data. After a few samples, the algorithm
should not be sensitive anymore to this a priori value.





Next: Exponential weighting
Up: THE LSL ALGORITHM
Previous: Recursions: order updating
Stanford Exploration Project
1/13/1998
![]() and rk,T-1(T). Their derivation is long, and I refer to
Lee et al. (1981) for an elegant proof. These authors use two other
intermediate variables, the angles
and rk,T-1(T). Their derivation is long, and I refer to
Lee et al. (1981) for an elegant proof. These authors use two other
intermediate variables, the angles ![]() , and
, and ![]() ;
especially,
;
especially, ![]() is defined as:
is defined as:
![]()