Next: FOURIER DOMAIN ALGORITHMS
Up: Biondi: Wave-equation algorithms on
Previous: Introduction
Fortran 90 is a new Fortran standard
that has been implemented on a few massively
parallel computers and a few vector computers.
The main advance of Fortran 90, with respect to Fortran 77,
is that arrays are treated as first-class objects.
Arrays, or sections of arrays, can be referenced in a single
statement,
and a whole set of intrinsic
functions are defined for complex manipulations of array objects.
The operations on the data expressed by the array statements,
or array functions,
are intrinsically parallel, and thus they can be efficiently
compiled for execution on a parallel hardware.
Using Fortran 90, the Geophysicist can express mathematical relations
in a high-level language, while the compiler and the system software
take care of parallelizing the execution of his program.
However,
the algorithms and the programs must still be designed carefully
if good performance is to be obtained.
The first issue to be addressed
when implementing algorithms on a massively
parallel computer is minimizing the
cost of interprocessor communications.
Massively parallel computers have the memory distributed among
many processors; the processors are linked together by a communication
network, which may have varying topology
(hypercube, 2-D mesh, etc ...).
Because computations can be performed only
when all the operands are local to a processor,
interprocessor communications are needed when the
required data do not reside in the memory of one
processor.
If the ratio between the time spent performing floating point operations
and the time spent moving data among processors is too low,
the performance of a parallel computer may be disappointing.
To minimize the time spent in communication
the user can determine
an ``optimal'' mapping
of the data into the memory of the processors.
The implementation of Fortran 90 on the Connection
Machine allows the user to specify the data layout with
a simple compiler directive.
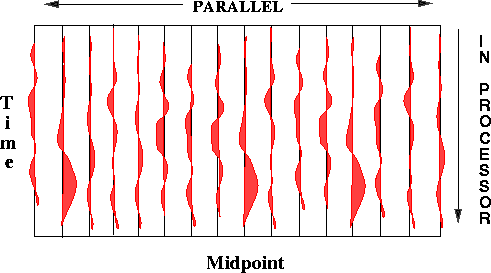
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example of how seismic
data can be mapped into processors memory.
The layout shown is the one used for the
Kirchhoff migration algorithm described in the final section of this paper.
The traces in a common-offset section are stored locally
in the memory of each processor, while the midpoint direction
is parallel. Because of this choice of data mapping
the generalized moveout operation that is in the innermost loop
of Kirchhoff migration can be performed
without inter-processor communications,
and the algorithm performs very well.
shows an example of how seismic
data can be mapped into processors memory.
The layout shown is the one used for the
Kirchhoff migration algorithm described in the final section of this paper.
The traces in a common-offset section are stored locally
in the memory of each processor, while the midpoint direction
is parallel. Because of this choice of data mapping
the generalized moveout operation that is in the innermost loop
of Kirchhoff migration can be performed
without inter-processor communications,
and the algorithm performs very well.
layout
Figure 1 The ``optimal'' mapping of a common-offset section into the processors' memory for Kirchhoff migration.

The most of the algorithms need inter-processor communication
even if the data have been
correctly mapped.
When communication is needed, it is
important that a fast type of communication is used.
On the Connection Machine, there are three types of
communication between processors: nearest neighbor,
global, and general communication.
The nearest neighbor and the global
communications are the fastest, and thus the most
desirable to use.
In Fortran 90,
the communications are expressed at a high level
as operations on the data arrays, or on elements of data arrays.
The compiler takes care of translating these Fortran statements
into the appropriate lower level communication functions.
The type of communication that is performed for executing
a specific Fortran 90 instruction depends on the data mapping,
as well as on the instruction itself.
Therefore,
the user
can control the type of communications
performed during the execution of his program by selecting
the ``optimal'' data layout
and by using the ``correct'' array operations.
The second basic principle for writing efficient
parallel programs is to keep the maximum number of
processors busy at all times.
The first way to
avoid idle processors is to have a
problem large enough compared to the size of the computer
at hand. In general, massively parallel computers
are not good at solving small problems.
Recursion along one of the parallel axes can be a cause of severe
load balancing problems.
Performing special
computations in the boundary regions of a finite-difference grid
is another situation where processor time
could be wasted, if the boundary conditions are not carefully designed.
There is no general recipe for avoiding load unbalancing, but
the most of the time the problem can be solved by
changing the data mapping and/or modifying the
algorithm. In extreme cases, the data can be redistributed among
the processors to balance the computational load,
at the expense of extra communications.
In the next section I begin my review of wave-equation algorithms
with Fourier domain methods.





Next: FOURIER DOMAIN ALGORITHMS
Up: Biondi: Wave-equation algorithms on
Previous: Introduction
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example of how seismic
data can be mapped into processors memory.
The layout shown is the one used for the
Kirchhoff migration algorithm described in the final section of this paper.
The traces in a common-offset section are stored locally
in the memory of each processor, while the midpoint direction
is parallel. Because of this choice of data mapping
the generalized moveout operation that is in the innermost loop
of Kirchhoff migration can be performed
without inter-processor communications,
and the algorithm performs very well.
shows an example of how seismic
data can be mapped into processors memory.
The layout shown is the one used for the
Kirchhoff migration algorithm described in the final section of this paper.
The traces in a common-offset section are stored locally
in the memory of each processor, while the midpoint direction
is parallel. Because of this choice of data mapping
the generalized moveout operation that is in the innermost loop
of Kirchhoff migration can be performed
without inter-processor communications,
and the algorithm performs very well.