Finding phase velocities and polarization vectors

When considering plane waves propagating an a homogeneous anisotropic medium it is convenient to use the Christoffel equations for an anisotropic medium. These equations:

 

 $$\lbrace~k_{iM}~C_{ML}~k_{Lj}~~-~~\rho{\omega}^2~\rbrace~~u_j~~=~~0~,$$

are the equations of motion of an elastic anisotropic medium, represented in the Fourier domain. Here C_ML is the stiffness matrix in compressed notation and k_iM, k_Lj ,$\omega$ denote the Fourier representations of spatial and temporal derivatives. $\rho_{ij}$ is the density tensor, u_j is the particle displacement. If we write the derivative matrices as functions of slowness rather than wavenumber we have,

 

 $$\left(~p_{iM}~C_{ML}~p_{Lj}~~-~~\rho~\right)~{\omega}^2~u_j~~=~~0~,$$

For the general anisotropic case C_ML has 21 independent elements. In the monoclinic case C_ML has 13 independent elements.

In equation  we can write p_iM C_ML p_Lj as a product of matrices:

$$\pmatrix{p_x&0&0&0&p_z&p_y\cr 0&p_y&0&p_z&0&p_x\cr 0&0&p_z... ...&0\cr 0&0&p_z\cr 0&p_z&p_y\cr p_z&0&p_x\cr p_y&p_x&0\cr}~.$$

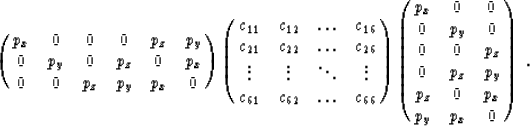
The result of the product is a 3x3 matrix a_ij. The Christoffel equation can be written now in the form:

$$\pmatrix{a_{11}-\rho & a_{12} & a_{13}\cr a_{12} & a_{22}-\... ..._{23} & a_{33}-\rho \cr} \pmatrix{a_1\cr a_2\cr a_3\cr} = 0$$

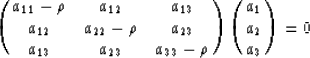
This system of equations has solutions when it's determinant vanishes. In general this requires solution of a sixth order polynomial in p_x,p_y,p_z. To find the vertical slowness for a given pair of horizontal slownesses p_x,p_y I must find the roots of a sextic in p_z. If the system has monoclinic symmetry the equations are somewhat simpler. The matrix elements in equation  only have terms in p_z² so the roots may be found by solving a cubic equation in p_z².

Solving the system equation  using the previously calculated roots gives the corresponding polarization vectors ${\bf a}$. I separate the wavetypes into up- and downgoing solutions by examining the energy flow direction, the Poynting vector.