Explicit schemes

Depth extrapolation is performed using the equation,

$$P(z+\delta z) = P(z) + \left.{\partial P\over\partial z}\right\vert _z \delta z\,.$$

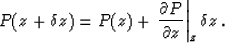
The square root in equation 1 can be approximated by a truncated series expansion. e.g.

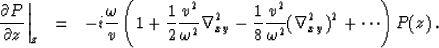$$\begin{eqnarray} \left. {\partial P\over\partial z}\right\vert _z & = & - i { \o... ...8}{v^2\over\omega^2}( \nabla_{xy}^2 )^2 + \cdots \right) P(z)\,.\end{eqnarray}$$ (2)

Explicit schemes are very simple to implement. On a regular grid the Laplacian operator can be implemented as a convolutional operator. This is very efficient on a mesh connected multiprocessor such as the Connection Machine.

The problem with explicit schemes is that, in general, they are unstable. Hale (1990) has demonstrated that unconditionally stable explicit operators can be created; however, these operators tend to be long so the convolution is expensive.