Implicit schemes

Most implicit schemes are based on a Crank-Nicholson formulation of the extrapolation problem. This method calculates a centered finite difference approximation to the z-derivative and averages the right hand side of the equation over the two depths:

$${ p_{z+\delta z} - p_z \over {\delta z}} \ =\ - i { \omega \... ...nabla_{xy}^2} \left( { p_{z+\delta z} + p_z \over 2 }\right)\,.$$

The square root is usually approximated by a continued fractions approximation. The standard $45^\circ$ approximation gives the following equations in retarded coordinates:

$${ q_{z+\delta z} - q_z \over {\delta z}} \ =\ {{ -i {v\over... ...la_{xy}^2 }} \left( { q_{z+\delta z} + q_z \over 2 } \right)\,.$$

When terms in q_z and $q_{z+\delta z}$ are gathered together, we obtain the following equation.

$$\left[1+\left( {v\over{2\omega}}^2 + i{v\over{2\omega}}\delt... ...v\over{2\omega}}\delta z \right) \nabla_{xy}^2 \right] q_{z}\,.$$

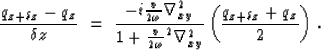
This problem is now in the form of a set of linear equations Ax=y. If the second-order-in-space finite difference operator is used to evaluate the Laplacian, the matrix A is pentadiagonal. Direct methods, such as Gaussian elimination, may be used to solve the system. For the particular structure of the system a block-Gaussian-elimination scheme may be used. For an $n\times n$ grid of data in x and y the operation count for the direct solution is O(n²). However, this method does not vectorize or parallelize well because of recursions in the algorithm. Methods that are more suitable for vectorization, such as block-cyclic-reduction, have a higher operation count, $O(n^2\log n)$. These costs are usually considered too high for routine application in seismic data processing. If a more accurate Laplacian operator is used the operator A will have a more thickly-banded structure and the cost of the direct solution will be higher.

Because of the high cost, this system is not usually solved in 3-D migration algorithms. Instead, a ``splitting'' approximation is made and the equations are rewritten in an approximate form that produces two sets of tridiagonal equations (Claerbout, 1985). However, the splitting approximation is not an isotropic approximation. If a time slice is made of the impulse response of the migration algorithm the wavefront is not circular. Waves propagating at $45^\circ$ to the computational grid travel slower than those along the axes of the grid. Hence, we would prefer to find a method that solves the pentadiagonal system.