Lateral velocity variation

When the velocity varies laterally, the matrix M in the extrapolation operator at equation (7) has coefficients which varies along the diagonal, but we can still derive a symmetric matrix (Godfrey et al., 1979). The symmetry property, which will guarantee the unconditional stability, can be obtained by putting the velocity term on both sides as follows

$${\partial \over \partial z} P = -{1\over \sqrt{v}}[-\omega^2... ...tial x}v^2{\partial \over \partial x}]^{1/2}{1\over \sqrt{v}} P$$ (20)

Now the small block matrices which are located along the diagonal in split matrices M_e and M_o will have a symmetric form

$$E =\Delta z \left( \begin{array} {cc} a&c\\ c&b\end{array} \right),$$

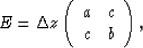
where

$$a=-{i\over 2}({\omega \over v(x)} -{v^2(x)+v^2(x-1) \over 2 v(x)\omega \Delta x^2}),$$

$$b=-{i\over 2}({\omega \over v(x+1)} -{v^2(x+1)+v^2(x) \over 2 v(x+1)\omega \Delta x^2}),$$

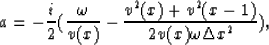
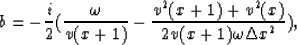
and

$$c=-i{v(x)^2 \over \sqrt{v(x+1)v(x)}2\omega \Delta x^2}.$$

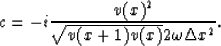
The eigenvalues of 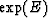$\exp(E)$ are given by

$$\lambda=\exp\left({a + b \pm \sqrt{(a-b)^2+4c^2} \over 2}\right)$$

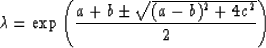
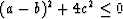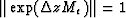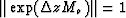and lie on the unit circle since a and b are imaginary, and $(a-b)^2 + 4c^2 \leq 0$.It follows that the matrix norms $\Vert\exp(\Delta z M_e)\Vert = 1$and $\Vert\exp(\Delta z M_o)\Vert = 1$.To prove the unconditional stability of the algorithm we need only show that 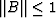$\Vert B\Vert\leq 1$. This follows immediately since 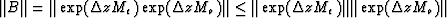$\Vert B\Vert=\Vert\exp(\Delta z M_e) \exp(\Delta z M_o)\Vert \leq\Vert\exp(\Delta z M_e)\Vert\Vert\exp(\Delta z M_o)\Vert$, each of which is unity according to the preceding argument.