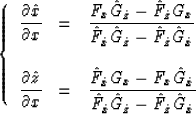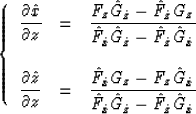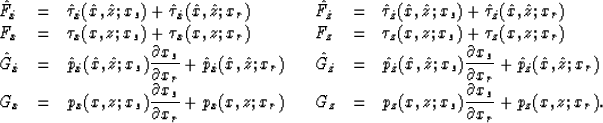Next: CALCULATING THE OPERATORS
Up: REVIEW
Previous: Kinematic relations
To use a finite-difference approach, we need to find the expressions
for partial derivatives:
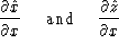
or
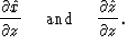
In my preceding paper (Zhang,1990b), I showed that
| 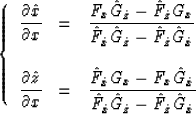 |
(3) |
and
| 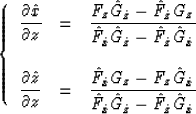 |
(4) |
where
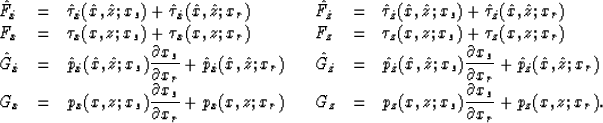
If the traveltime table is calculated with polar coordinates 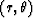 ,instead of Cartesian coordinates (x,z), then we can simply change x and z
in equations (3) and (4) to
,instead of Cartesian coordinates (x,z), then we can simply change x and z
in equations (3) and (4) to 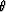 and
r, respectively.
and
r, respectively.
With equations (3) and (4), we can extrapolate
the operators in both the horizontal and vertical directions.
Because the operators are usually known at the surface, one can use
equation (4) to extrapolate the operators vertically
to each depth. The next section shows how this extrapolation is done.





Next: CALCULATING THE OPERATORS
Up: REVIEW
Previous: Kinematic relations
Stanford Exploration Project
12/18/1997
![]()
![]()