




Next: APPLICATIONS
Up: LINEAR OPTIMIZATION
Previous: Residual dip
We can apply the approximation in equation (10) to the objective
functions. For example, from equations (3)
and (7) we can derive
| ![\begin{displaymath}
\begin{array}
{lll}
E^0(t,x,\Delta p) & = & \displaystyle{\s...
...rtial t}j\Delta p \Delta x \right)\right]^2
\right\}\end{array}\end{displaymath}](img17.gif) |
(11) |
The optimal estimate of 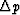 is the minimizer of this function.
Because the objective function is a quadratic function of the unknown
is the minimizer of this function.
Because the objective function is a quadratic function of the unknown
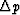 , one can use the standard least-squares techniques to find
the solution of this linear optimization problem:
, one can use the standard least-squares techniques to find
the solution of this linear optimization problem:
| ![\begin{displaymath}
\Delta p = \displaystyle{\displaystyle{\sum^{L_t}_{i=-L_t}}W...
...ystyle{\partial P \over \partial t}j\Delta x \right)^2 \right]}\end{displaymath}](img18.gif) |
(12) |
Once 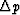 is found for each t, the pick can be improved
by using equation (9).
is found for each t, the pick can be improved
by using equation (9).





Next: APPLICATIONS
Up: LINEAR OPTIMIZATION
Previous: Residual dip
Stanford Exploration Project
12/18/1997
![\begin{displaymath}
\begin{array}
{lll}
E^0(t,x,\Delta p) & = & \displaystyle{\s...
...rtial t}j\Delta p \Delta x \right)\right]^2
\right\}\end{array}\end{displaymath}](img17.gif)
![\begin{displaymath}
\begin{array}
{lll}
E^0(t,x,\Delta p) & = & \displaystyle{\s...
...rtial t}j\Delta p \Delta x \right)\right]^2
\right\}\end{array}\end{displaymath}](img17.gif)
![\begin{displaymath}
\Delta p = \displaystyle{\displaystyle{\sum^{L_t}_{i=-L_t}}W...
...ystyle{\partial P \over \partial t}j\Delta x \right)^2 \right]}\end{displaymath}](img18.gif)