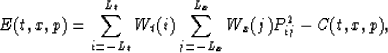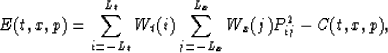Relations

We can achieve the optimal estimation by minimizing the functions in equations (3) and (4), or maximizing the functions in equations (5) and (6). Would we get an identical result if we use the two different methods? To answer this question, let us examine the relations between these objective functions:  

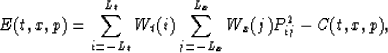$$E(t,x,p) = \sum^{L_t}_{i=-L_t}W_t(i)\sum^{L_x}_{j=-L_x}W_x(j)P^2_{ij}-C(t,x,p),$$ (7)

and

 

E_n(t,x,p) = 1-C_n(t,x,p). (8)

It is clear that, for the normalized objective functions, minimizing E_n(t,x,p) is completely equivalent to maximizing C_n(t,x,p). The first term on the right-hand side of equation (7) is the weighted energy of the subsection. This term usually maintains to be constant. Therefore, for unnormalized objective functions, we can draw a similar conclusion to that of the normalized objective functions. In view of the calculation of these functions, the coherence measures are easier to calculate than the error measures.