Next: Numerical instability problems
Up: Popovici : FD Traveltime
Previous: 3-D ALGORITHM
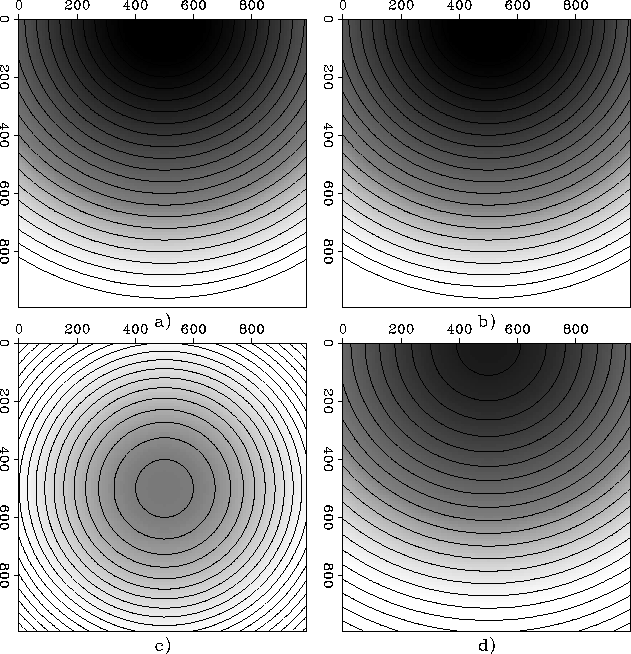
The first example shown in Figure 2 represents sections
through a 3-D traveltime field
for a constant velocity of 2 km/s.
The 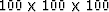 grid is evenly sampled
laterally and in depth, with a sample interval of 10 m.
The source is situated at the surface, in the middle of
the plane. Figure 2a and 2b represent vertical orthogonal planes
passing through the source. The vertical plane in
Figure 2d is offset with a distance
(X=300 m) from the source. Figure 2c shows the values
of the traveltime field on a
horizontal surface passing through the middle of the cube.
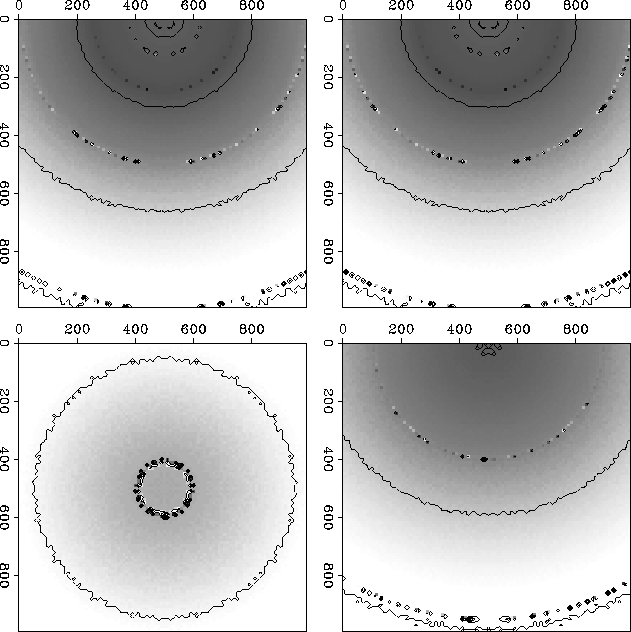
Figure 3 displays the difference between the analytical solution
and the computed traveltime field for each panel shown in Figure 2.
The distribution of the errors is shown through lines of
constant value. The errors accumulate with distance from the source.
The values of the absolute error on each surface
(of order 10-6) are
shown in Figure 4.
grid is evenly sampled
laterally and in depth, with a sample interval of 10 m.
The source is situated at the surface, in the middle of
the plane. Figure 2a and 2b represent vertical orthogonal planes
passing through the source. The vertical plane in
Figure 2d is offset with a distance
(X=300 m) from the source. Figure 2c shows the values
of the traveltime field on a
horizontal surface passing through the middle of the cube.
Figure 3 displays the difference between the analytical solution
and the computed traveltime field for each panel shown in Figure 2.
The distribution of the errors is shown through lines of
constant value. The errors accumulate with distance from the source.
The values of the absolute error on each surface
(of order 10-6) are
shown in Figure 4.
Ray3Dmc
Figure 1 Traveltime
map for a constant 3-D velocity model (1000 m each side) with the source
at the surface. a) Vertical section through the middle
of the cube for constant X. b) Vertical section through the
middle of the cube for constant Y. c) Horizontal section through
the middle of the cube for constant Z. d) Vertical section off the
middle of the cube for constant X (X=800 m).
 Diff3Dmc
Diff3Dmc
Figure 2 Difference
between the computed traveltime map and the analytical solution
for a constant velocity model. Each figure represents the
difference between the analytical solution and the corresponding
panel in Figure 2. The error accumulates with distance from the source.

GraphDiffmc
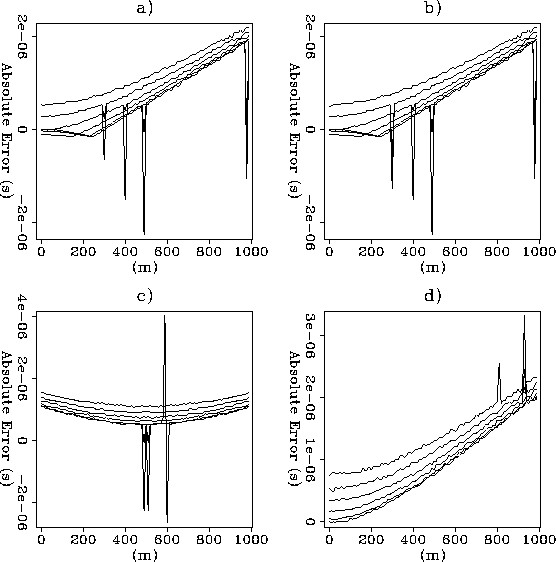
Figure 3 Errors
in the finite-difference calculations. Each panel shows several curves
which represent the absolute error across the corresponding
sections in Figure 3.

The constant velocity model is a poor example to examine a
finite-difference algorithm based on the
Engquist-Osher scheme, as the functions 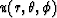 and
and
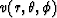 are zero on spherical shells of constant
radius r. Therefore the errors in the constant velocity case
are merely due to numerical integration and interpolation
from cartesian to spherical coordinates.
are zero on spherical shells of constant
radius r. Therefore the errors in the constant velocity case
are merely due to numerical integration and interpolation
from cartesian to spherical coordinates.
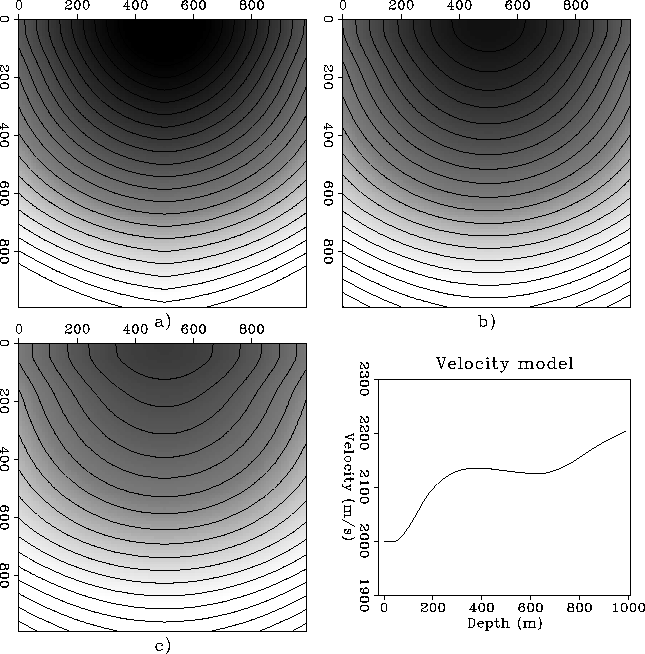
Figure 5 shows results for a traveltime field in a depth
variable velocity medium.
the computations are done on the same 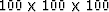 grid with a spacing of 10 m.
The three panels shown in Figures 5a, 5b and 5c represent vertical
planes situated at increasing distance from the source.
Figure 5d displays the depth variable velocity model.
The 3-D algorithm is an order of magnitude more unstable than
the 2-D algorithm for comparable grid parameters in spherical,
and cylindrical coordinates respectively.
The instability problems disappear for smaller grid intervals
in spherical coordinates,
but one is limited by the amount of computer memory which
can be allocated for an increasing number of grid points.
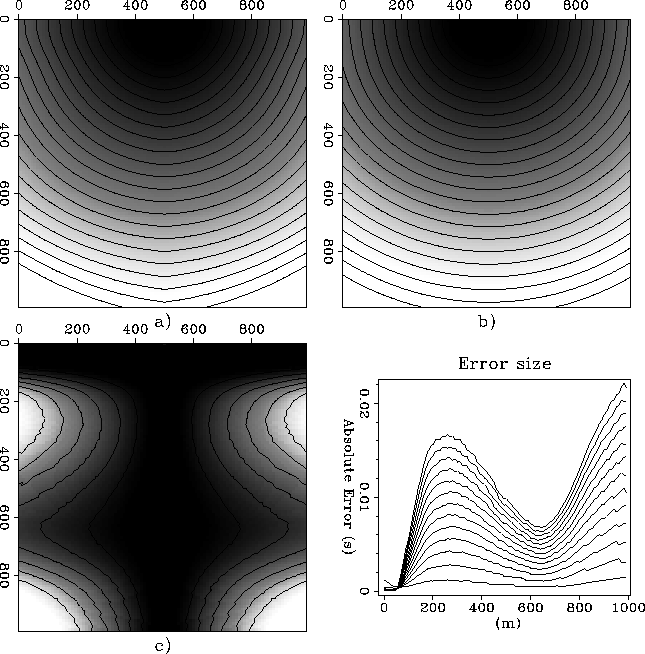
The absolute error is not negligible at the sides of the panel,
as can be seen from Figure 6c and 6d. Maximum values for
the error appear on the edges of the model studied, at
higher values of the traveltime field. The traveltimes in the
3-D model tend to be higher, as the difference between the 3-D
section and the 2-D section is always positive.
grid with a spacing of 10 m.
The three panels shown in Figures 5a, 5b and 5c represent vertical
planes situated at increasing distance from the source.
Figure 5d displays the depth variable velocity model.
The 3-D algorithm is an order of magnitude more unstable than
the 2-D algorithm for comparable grid parameters in spherical,
and cylindrical coordinates respectively.
The instability problems disappear for smaller grid intervals
in spherical coordinates,
but one is limited by the amount of computer memory which
can be allocated for an increasing number of grid points.
The absolute error is not negligible at the sides of the panel,
as can be seen from Figure 6c and 6d. Maximum values for
the error appear on the edges of the model studied, at
higher values of the traveltime field. The traveltimes in the
3-D model tend to be higher, as the difference between the 3-D
section and the 2-D section is always positive.
Ray3Dm1
Figure 4 Traveltime map
for a 3-D depth variable velocity model (1000 m each side) with
the source in the middle of the top surface. a) Vertical section
through the source. b) Vertical section with offset (X=250 m)
from the source. c) Vertical section with offset (X=450 m) from
the source. d) Velocity model.

Ray3Ddiff
Figure 5 Comparison between
3-D and a 2-D finite-difference traveltime map for the depth
variable velocity model shown in Figure 5d. a) Vertical section through the
source in the 3-D model. b) 2-D traveltime field for the same
depth variable velocity model. c) Difference between the 3-D
traveltime field and the 2-D traveltime field. d) Absolute
errors for the 3-D vs. 2-D difference.






Next: Numerical instability problems
Up: Popovici : FD Traveltime
Previous: 3-D ALGORITHM
Stanford Exploration Project
12/18/1997
![]() grid is evenly sampled
laterally and in depth, with a sample interval of 10 m.
The source is situated at the surface, in the middle of
the plane. Figure 2a and 2b represent vertical orthogonal planes
passing through the source. The vertical plane in
Figure 2d is offset with a distance
(X=300 m) from the source. Figure 2c shows the values
of the traveltime field on a
horizontal surface passing through the middle of the cube.
Figure 3 displays the difference between the analytical solution
and the computed traveltime field for each panel shown in Figure 2.
The distribution of the errors is shown through lines of
constant value. The errors accumulate with distance from the source.
The values of the absolute error on each surface
(of order 10-6) are
shown in Figure 4.
grid is evenly sampled
laterally and in depth, with a sample interval of 10 m.
The source is situated at the surface, in the middle of
the plane. Figure 2a and 2b represent vertical orthogonal planes
passing through the source. The vertical plane in
Figure 2d is offset with a distance
(X=300 m) from the source. Figure 2c shows the values
of the traveltime field on a
horizontal surface passing through the middle of the cube.
Figure 3 displays the difference between the analytical solution
and the computed traveltime field for each panel shown in Figure 2.
The distribution of the errors is shown through lines of
constant value. The errors accumulate with distance from the source.
The values of the absolute error on each surface
(of order 10-6) are
shown in Figure 4.
![]() and
and
![]() are zero on spherical shells of constant
radius r. Therefore the errors in the constant velocity case
are merely due to numerical integration and interpolation
from cartesian to spherical coordinates.
are zero on spherical shells of constant
radius r. Therefore the errors in the constant velocity case
are merely due to numerical integration and interpolation
from cartesian to spherical coordinates.
![]() grid with a spacing of 10 m.
The three panels shown in Figures 5a, 5b and 5c represent vertical
planes situated at increasing distance from the source.
Figure 5d displays the depth variable velocity model.
The 3-D algorithm is an order of magnitude more unstable than
the 2-D algorithm for comparable grid parameters in spherical,
and cylindrical coordinates respectively.
The instability problems disappear for smaller grid intervals
in spherical coordinates,
but one is limited by the amount of computer memory which
can be allocated for an increasing number of grid points.
The absolute error is not negligible at the sides of the panel,
as can be seen from Figure 6c and 6d. Maximum values for
the error appear on the edges of the model studied, at
higher values of the traveltime field. The traveltimes in the
3-D model tend to be higher, as the difference between the 3-D
section and the 2-D section is always positive.
grid with a spacing of 10 m.
The three panels shown in Figures 5a, 5b and 5c represent vertical
planes situated at increasing distance from the source.
Figure 5d displays the depth variable velocity model.
The 3-D algorithm is an order of magnitude more unstable than
the 2-D algorithm for comparable grid parameters in spherical,
and cylindrical coordinates respectively.
The instability problems disappear for smaller grid intervals
in spherical coordinates,
but one is limited by the amount of computer memory which
can be allocated for an increasing number of grid points.
The absolute error is not negligible at the sides of the panel,
as can be seen from Figure 6c and 6d. Maximum values for
the error appear on the edges of the model studied, at
higher values of the traveltime field. The traveltimes in the
3-D model tend to be higher, as the difference between the 3-D
section and the 2-D section is always positive.