




Next: 3-D TRAVELTIME MAPS
Up: Popovici : FD Traveltime
Previous: An insight into the
In 3-D the eikonal equation is
where
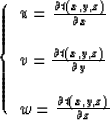
For a spherical-coordinates system
| 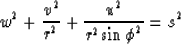 |
(9) |
where
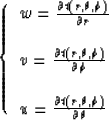
The cross derivative equation (4) is transformed into
the spherical coordinates system
| 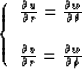 |
(10) |
The finite-difference equivalent of equation (5) is
the system
| 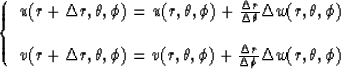 |
(11) |
which is used to advance the stencil for a new radial increment.
Once the values of the functions 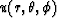 and
and
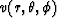 are known on the spherical
front with constant radius (
are known on the spherical
front with constant radius (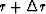 ),
the third function
),
the third function 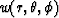 can be calculated using the eikonal equation
can be calculated using the eikonal equation
| 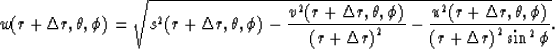 |
(12) |
The value of the traveltime is found by integration:
![\begin{displaymath}
t(r+\Delta r,\theta,\phi)=t(r,\theta,\phi)+{\Delta r \over 2}
[w(r+\Delta r,\theta,\phi)+w(r,\theta,\phi)].\end{displaymath}](img34.gif)
In equation (11), the Engquist-Osher scheme is applied twice, once for
calculating the values of 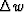 across three points
of consecutive values of
across three points
of consecutive values of 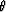 , and second for calculating
the values of
, and second for calculating
the values of 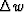 across three consecutive values
of
across three consecutive values
of 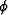 .The computational front advances in spherical shells, and on
each shell the computations advance a circle at a
time.
The angle
.The computational front advances in spherical shells, and on
each shell the computations advance a circle at a
time.
The angle 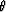 is the horizontal angle while
the angle
is the horizontal angle while
the angle 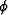 is the vertical angle.
The Engquist-Osher scheme is applied along each
three consecutive points on the circle with constant vertical
angle
is the vertical angle.
The Engquist-Osher scheme is applied along each
three consecutive points on the circle with constant vertical
angle 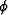 to determine
to determine 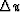 from the equation
from the equation
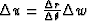 .For each circle of constant vertical angle
.For each circle of constant vertical angle 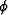 the
Engquist-Osher scheme is applied for three points
(
the
Engquist-Osher scheme is applied for three points
(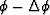 ),
), 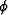 and (
and (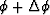 ), which are
perpendicular on the circle in the
), which are
perpendicular on the circle in the 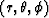 coordinates.
The scheme is completely vectorizable.
coordinates.
The scheme is completely vectorizable.





Next: 3-D TRAVELTIME MAPS
Up: Popovici : FD Traveltime
Previous: An insight into the
Stanford Exploration Project
12/18/1997
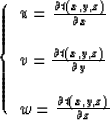
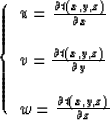
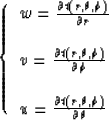
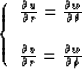
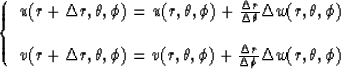
![]()