Absorbing boundaries

The absorbing boundary conditions in the sides and bottom of the model are based in the method described by Cerjan et al. (1985), which is at the same time simple and suitable for implementation in a parallel architecture. An N-grid-points-thick absorbing region covers the three absorbing regions. Following each time step, the wavefield inside this region is multiplied by a Gaussian damping function $G = \exp -[(N-i)/\sigma_N]^2.$, where i is the distance (in grid-points units) from the boundary. The total attenuation applied to a wavefield propagating with an extreme velocity of one grid-point per time-step is  

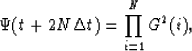$$\Psi(t+2N\Delta t) = \prod_{i=1}^N G^2(i),$$ (9)

as illustrated in Figure . Stable modeling requires velocities smaller than that, resulting in a cumulative attenuation always stronger than that described by equation (9). One of the nice things about the parallel architecture is the facility provided by the natural circular boundary conditions. No special treatment is required for the two sides of the model because the waves transmitted from one boundary to the other are sufficiently attenuated to have any significant effect.

 

absorbing
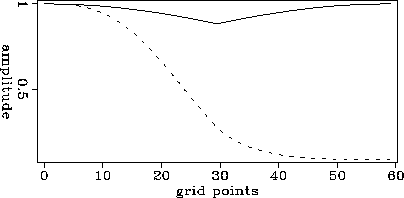
Figure 2 The continuous curve represents the attenuation applied at each grid point inside the absorbing region, while the dashed line represents the cumulative attenuation suffered by a wavefield propagating with a velocity of one-gridpoint per time-step as described by equation ().