




Next: References
Up: Claerbout: Eigenvectors for missing
Previous: GRADIENT
Finally, I introduce the specialized notation I like
for optimization manipulations.
First, I omit bold on vectors.
Second, when a vector is transformed by the operator 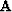 ,I denote the transformed vector by an upper-case letter.
Thus
,I denote the transformed vector by an upper-case letter.
Thus 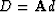 and
and 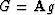 .Let the scalar
.Let the scalar  denote the distance moved along the gradient.
In this notation, perturbations of
denote the distance moved along the gradient.
In this notation, perturbations of 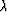 are
are
| 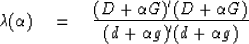 |
(6) |
A steepest descent method amounts to:
- 1.
- Find the gradient
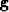 using (5)
using (5)
- 2.
- Compute
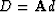 and
and 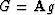
- 3.
- Maximize the ratio of scalars in (6)
by any crude method such as interval division.
- 4.
- Repeat.
A conjugate-gradient-like method is like the steepest descent method
supplementing the gradient by another vector,
the vector of the previous step.
Michael Saunders suggested the Pollack-Ribier (sp) method
and gave me a Fortran subroutine for the line search.





Next: References
Up: Claerbout: Eigenvectors for missing
Previous: GRADIENT
Stanford Exploration Project
12/18/1997