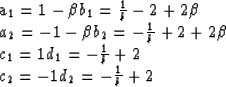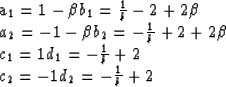Next: NMO CORRECTION AND SPECTRA
Up: Ji and Claerbout: Trace
Previous: REVIEW OF CLAERBOUT'S RECURSIVE
The strategy for interpolation of missing traces is an inversion which
determines the missing traces so as to minimize the high-dip-pass filtered
output.
For optimization, we use a conjugate-gradient algorithm.
Conjugate-gradient inversion is an iterative method in which each
iteration involves the application of a forward operator and
its transpose.
The forward operator of a recursive dip filter can be represented as
| <I>AqI> = <I>BpI> |
<I>orI> |
<I>qI>=<I>A-1BpI>, |
(5) |
where A and B are matrices as follows:
| b1 |
a1 |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
|
| a1 |
b1 |
a1 |
. |
. |
. |
. |
. |
. |
. |
. |
. |
|
| . |
a1 |
b1 |
a1 |
. |
. |
. |
. |
. |
. |
. |
. |
|
| . |
. |
a1 |
b1 |
. |
. |
. |
. |
. |
. |
. |
. |
|
| b2 |
a2 |
. |
. |
b1 |
a1 |
. |
. |
. |
. |
. |
. |
|
| a2 |
b2 |
a2 |
. |
a1 |
b1 |
a1 |
. |
. |
. |
. |
. |
|
| . |
a2 |
b2 |
a2 |
. |
a1 |
b1 |
a1 |
. |
. |
. |
. |
|
| . |
. |
a2 |
b2 |
. |
. |
a1 |
b1 |
. |
. |
. |
. |
|
| . |
. |
. |
. |
b2 |
a2 |
. |
. |
b1 |
a1 |
. |
. |
|
| . |
. |
. |
. |
a2 |
b2 |
a2 |
. |
a1 |
b1 |
a1 |
. |
|
| . |
. |
. |
. |
. |
a2 |
b2 |
a2 |
. |
a1 |
b1 |
a1 |
|
| . |
. |
. |
. |
. |
. |
a2 |
b2 |
. |
. |
a1 |
b1 |
|
| q11 |
|
| q12 |
|
| q13 |
|
| q14 |
|
| q21 |
|
| q22 |
|
| q23 |
|
| q24 |
|
| q31 |
|
| q32 |
|
| q33 |
|
| q34 |
|
=
| d1 |
c1 |
. |
. |
. |
. |
. |
. |
. |
. |
. |
. |
|
| c1 |
d1 |
c1 |
. |
. |
. |
. |
. |
. |
. |
. |
. |
|
| . |
c1 |
d1 |
c1 |
. |
. |
. |
. |
. |
. |
. |
. |
|
| . |
. |
c1 |
d1 |
. |
. |
. |
. |
. |
. |
. |
. |
|
| d2 |
c2 |
. |
. |
d1 |
c1 |
. |
. |
. |
. |
. |
. |
|
| c2 |
d2 |
c2 |
. |
c1 |
d1 |
c1 |
. |
. |
. |
. |
. |
|
| . |
c2 |
d2 |
c2 |
. |
c1 |
d1 |
c1 |
. |
. |
. |
. |
|
| . |
. |
c2 |
d2 |
. |
. |
c1 |
d1 |
. |
. |
. |
. |
|
| . |
. |
. |
. |
d2 |
c2 |
. |
. |
d1 |
c1 |
. |
. |
|
| . |
. |
. |
. |
c2 |
d2 |
c2 |
. |
c1 |
d1 |
c1 |
. |
|
| . |
. |
. |
. |
. |
c2 |
d2 |
c2 |
. |
c1 |
d1 |
c1 |
|
| . |
. |
. |
. |
. |
. |
c2 |
d2 |
. |
. |
c1 |
d1 |
|
| p11 |
|
| p12 |
|
| p13 |
|
| p14 |
|
| p21 |
|
| p22 |
|
| p23 |
|
| p24 |
|
| p31 |
|
| p32 |
|
| p33 |
|
| p34 |
|
where
and the subscript and the superscript in pji and qji represent
offset-axis and time-axis indices respectively.
The transpose operator of equation (5) is defined by
In actual calculations, instead of inverting the matrix, we can
use a tridiagonal solver, as follows:
In the appendix, we list the program that applies the operator and
its conjugate operator, along with the result of the dot-product test
for demonstrating conjugacy (Claerbout, 1991).





Next: NMO CORRECTION AND SPECTRA
Up: Ji and Claerbout: Trace
Previous: REVIEW OF CLAERBOUT'S RECURSIVE
Stanford Exploration Project
12/18/1997