Let us suppose we have a one dimensional, continuous signal s(t) that has a finite time duration T. Within the time interval T, this signal can be represented by a Fourier series expansion as follows:
| |
(2) |
![]()
Let ![]() be a sequence of samples of this
signal. If one can reconstruct the original continuous signal from this
finite number of samples, then one can interpolate or resample this signal
arbitrarily. This reconstruction is possible
if the spectrum of the signal is band-limited, in other words, if the
Fourier series expansion in equation (2) has a finite number
of terms. With this assumption, equation (2) tells us that
the continuous signal can be fully described by a finite number of samples
of its spectrum. Thus, the key step of the reconstruction is to
estimate the spectrum.
be a sequence of samples of this
signal. If one can reconstruct the original continuous signal from this
finite number of samples, then one can interpolate or resample this signal
arbitrarily. This reconstruction is possible
if the spectrum of the signal is band-limited, in other words, if the
Fourier series expansion in equation (2) has a finite number
of terms. With this assumption, equation (2) tells us that
the continuous signal can be fully described by a finite number of samples
of its spectrum. Thus, the key step of the reconstruction is to
estimate the spectrum.
Substituting the known samples into equation (2) gives
| |
(3) |
![]()
![]()
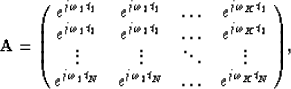
| (4) |
| |
(5) |
There exist many numerical algorithms for solving a general normal equation.
But the computation required is generally in an order of K3.
Fortunately, as we will see later, the matrix ![]() has a special
structure that makes it possible to solve equation with an order of
K2 operations.
has a special
structure that makes it possible to solve equation with an order of
K2 operations.