




Next: LOCAL WAVEFRONT EXTRAPOLATION
Up: Zhang: Local paraxial ray
Previous: Introduction
Ray tracing is a technique for finding the coordinates of a ray.
Suppose, by using this technique, that we find the coordinates of the ray.
We can then define a new orthogonal coordinate system (s,n),
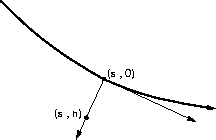
named ray-centered coordinates. As Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows,
the coordinate s measures the arc-length along the ray, and the coordinate
n is the normal distance from the ray at point s on the ray. Let us
denote the relations between Cartesian coordinates and ray-centered
coordinates as
shows,
the coordinate s measures the arc-length along the ray, and the coordinate
n is the normal distance from the ray at point s on the ray. Let us
denote the relations between Cartesian coordinates and ray-centered
coordinates as 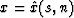 and
and 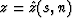 . Then, the coordinates
of the ray are
. Then, the coordinates
of the ray are 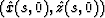 . The traveltime on any point of
the ray can be computed by integrating the slowness function along the
ray, as follows:
. The traveltime on any point of
the ray can be computed by integrating the slowness function along the
ray, as follows:
| 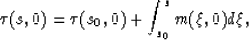 |
(1) |
where m(s,n) is the slowness function in ray-centered coordinates.
rccoor
Figure 1 Ray-centered coordinates.
|
|  |

The amplitude calculation is more complicated than the traveltime calculation.
Cervený et al. (1977) showed that the amplitude function along the ray
is related to a Jacobian function determined by
| ![\begin{displaymath}
J(s,0)=J(s_0,0)\exp[\int^s_{s_0}{M(\xi,0) \over m(\xi,0)}d\xi],\end{displaymath}](img5.gif) |
(2) |
where M(s,0) is the second-order partial derivative of the traveltime
with respect to n along the ray and can be found by solving the
dynamic ray-tracing equation
| 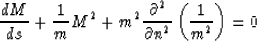 |
(3) |
along the ray.
To compute the traveltimes and amplitudes off but near the ray, we
use the paraxial ray approximation. The resulted traveltime is
| 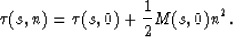 |
(4) |
The direction of a ray follows the direction of the traveltime gradient that
is determined by
| ![\begin{displaymath}
\nabla \tau(s,n)= \left[m(s,0)+{\partial m \over \partial n}...
...l M \over \partial s}n^2\right]\vec{\bf s}+
M(s,0)n\vec{\bf n},\end{displaymath}](img8.gif) |
(5) |
where 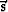 and
and 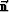 are unit vectors tangential and normal to
the ray at (s,0), respectively. Using the paraxial approximation
also yields
are unit vectors tangential and normal to
the ray at (s,0), respectively. Using the paraxial approximation
also yields
| ![\begin{displaymath}
M(s,n)=m(s,n){M(s,0) \over m(s,0)}\left[1-{1 \over 2}
{M^2(s,0) \over m^2(s,0)}n^2\right]\end{displaymath}](img11.gif) |
(6) |
and
| ![\begin{displaymath}
J(s,n)=J(s,0)\left[1+{M^2(s,0) \over 2m^2(s,0)}n^2\right].\end{displaymath}](img12.gif) |
(7) |
The next section explains how these equations are used in the local
paraxial ray method.





Next: LOCAL WAVEFRONT EXTRAPOLATION
Up: Zhang: Local paraxial ray
Previous: Introduction
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows,
the coordinate s measures the arc-length along the ray, and the coordinate
n is the normal distance from the ray at point s on the ray. Let us
denote the relations between Cartesian coordinates and ray-centered
coordinates as
shows,
the coordinate s measures the arc-length along the ray, and the coordinate
n is the normal distance from the ray at point s on the ray. Let us
denote the relations between Cartesian coordinates and ray-centered
coordinates as ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows,
the coordinate s measures the arc-length along the ray, and the coordinate
n is the normal distance from the ray at point s on the ray. Let us
denote the relations between Cartesian coordinates and ray-centered
coordinates as
shows,
the coordinate s measures the arc-length along the ray, and the coordinate
n is the normal distance from the ray at point s on the ray. Let us
denote the relations between Cartesian coordinates and ray-centered
coordinates as ![]() and
and ![]() . Then, the coordinates
of the ray are
. Then, the coordinates
of the ray are ![]() . The traveltime on any point of
the ray can be computed by integrating the slowness function along the
ray, as follows:
. The traveltime on any point of
the ray can be computed by integrating the slowness function along the
ray, as follows:
