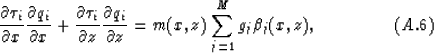Next: About this document ...
Up: Zhang: Tomography
Previous: References
In this appendix, I derive equations (13) and (15),
and the initial conditions associated with them.
The Cartesian coordinates of the trajectory of a ray are functions of
so-called ray coordinates (s,r), as follows:

where s measures the arc-length of the ray and r is the depth at which
the ray reaches the receiver well. Subscript i indicates the source number.
If we solve equation (A.1) for r,
we obtain a function 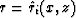 that has a constant value
along each ray. Consequently, the gradient directions of function
that has a constant value
along each ray. Consequently, the gradient directions of function
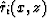 are orthogonal to rays.
Because the gradient directions of traveltime function
are orthogonal to rays.
Because the gradient directions of traveltime function 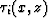 are
tangential to rays, we have the relation
are
tangential to rays, we have the relation 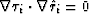 ,which, in two dimensions, yields
,which, in two dimensions, yields

At any receiver location, function 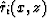 is equal to the depth
of the receiver, which acts as an initial condition required in solving
equation (A.2).
is equal to the depth
of the receiver, which acts as an initial condition required in solving
equation (A.2).
To derive equation (15), we first define
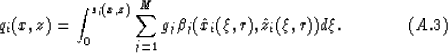
At the source location, si(x,z) is equal to zero; hence qi(x,z) is equal
to zero. At the receiver locations, si(x,z)=si(r). Comparing
equation (A.3) with equation (15), we can conclude that
qi(x,z) is equal to h(1)(r) at the receiver locations.
Now, what remains is
to show that qi(x,z) defined in equation (A.3) satisfies
the first-order linear partial differential equation (15).
To do so, we take the derivative of both sides of equation (A.3)
with respect to s, which yields
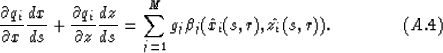
Functions 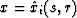 and
and 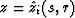 define the
Cartesian coordinates of the ray. They satisfy the ray equation as follows:
define the
Cartesian coordinates of the ray. They satisfy the ray equation as follows:
![\begin{displaymath}
\left\{
\begin{array}
{lll}
\displaystyle{dx \over ds} & = &...
...partial z}
\right] & = & m_z(x,z),\end{array}\right.
\eqno(A.5)\end{displaymath}](img51.gif)
where subscripts x and z denote partial derivatives with respect to
x and z, respectively.
Substituting these functions into equation (A.4) gives
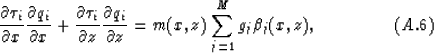
which is equation (15).





Next: About this document ...
Up: Zhang: Tomography
Previous: References
Stanford Exploration Project
12/18/1997
![]()
![]()
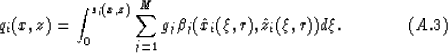
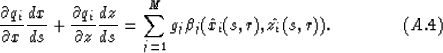
![\begin{displaymath}
\left\{
\begin{array}
{lll}
\displaystyle{dx \over ds} & = &...
...partial z}
\right] & = & m_z(x,z),\end{array}\right.
\eqno(A.5)\end{displaymath}](img51.gif)