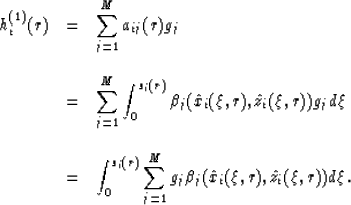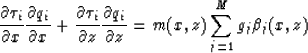Next: CONCLUSIONS
Up: FINITE DIFFERENCE METHODS
Previous: Computation of the gradient
The conjugate gradient vector has two parts. The first part 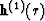 is related to the traveltime residuals, and the second part
is related to the traveltime residuals, and the second part 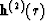 is related to the constraints. The computation of
is related to the constraints. The computation of 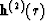 is simple
because matrix
is simple
because matrix  is known. We want to compute
is known. We want to compute 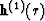 with a
finite difference method. The components of
with a
finite difference method. The components of 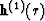 are as follows:
are as follows:
| 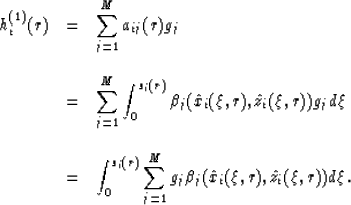 |
(14) |
It is shown in Appendix A that if we solve the first-order linear PDE
| 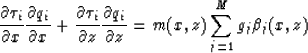 |
(15) |
with the initial condition that qi(x,z) is equal to zero at the source
location, then h(1)i(r) is equal to qi(x,z) at the receiver
locations. Equation (15) has a form similar to the eikonal equation;
hence we can use the algorithm for the traveltime calculation,
after being slightly modified, to solve it.





Next: CONCLUSIONS
Up: FINITE DIFFERENCE METHODS
Previous: Computation of the gradient
Stanford Exploration Project
12/18/1997
![]() is related to the traveltime residuals, and the second part
is related to the traveltime residuals, and the second part ![]() is related to the constraints. The computation of
is related to the constraints. The computation of ![]() is simple
because matrix
is simple
because matrix ![]() is known. We want to compute
is known. We want to compute ![]() with a
finite difference method. The components of
with a
finite difference method. The components of ![]() are as follows:
are as follows: