




Next: Computation of the gradient
Up: FINITE DIFFERENCE METHODS
Previous: The computation of traveltimes
The elements of matrix 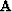 are the derivatives of the traveltimes
with respect to the slowness model parameters. Let us define
are the derivatives of the traveltimes
with respect to the slowness model parameters. Let us define
| 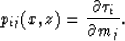 |
(8) |
Taking the derivatives of both sides of the eikonal equation with respect
to mj gives
| 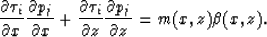 |
(9) |
If we assume that 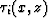 has been
computed by solving the eikonal equation, then equation (9)
is a first-order
linear partial differential equation (PDE). Because the traveltime
at the source location is always zero no matter how the slowness model
changes, equation (9) should be solved with the initial condition
that pij(x,z)=0 at the source location.
Evaluating the function pij(x,z)
at receiver locations gives the elements of matrix
has been
computed by solving the eikonal equation, then equation (9)
is a first-order
linear partial differential equation (PDE). Because the traveltime
at the source location is always zero no matter how the slowness model
changes, equation (9) should be solved with the initial condition
that pij(x,z)=0 at the source location.
Evaluating the function pij(x,z)
at receiver locations gives the elements of matrix 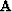 .
.





Next: Computation of the gradient
Up: FINITE DIFFERENCE METHODS
Previous: The computation of traveltimes
Stanford Exploration Project
12/18/1997
![]() are the derivatives of the traveltimes
with respect to the slowness model parameters. Let us define
are the derivatives of the traveltimes
with respect to the slowness model parameters. Let us define