




Next: THE SPLIT-STEP FOURIER METHOD
Up: Popovici : PSPI and
Previous: INTRODUCTION
The derivation of the Phase Shift Plus Interpolation (PSPI) algorithm
starts with the scalar wave equation
| 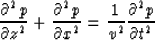 |
(1) |
where p=p(x,z,t) is the pressure field and v=v(x,z) is the earth
velocity.
The pressure field p(x,z,t) is a finite function and can be therefore
expressed as a double Fourier series
| 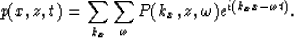 |
(2) |
Substituting the equation (2) in equation (1) we obtain
![\begin{displaymath}
{\sum_{k_x} \sum_{\omega}[ {\partial^2 P(k_x,z,\omega) \over...
...a^2 \over v^2(x,z)} P(k_x,z,\omega)]
e^{i(k_x x-\omega t)}= 0} \end{displaymath}](img3.gif)
which after considering only the equation inside the square parenthesis
becomes
| 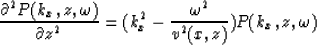 |
(3) |
valid for all the values of kx and 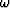 .The problem is that in this form, the x coordinate in the pressure
field is Fourier transformed and there is no direct
correspondence between a point in the medium of coordinates (x,z),
the velocity v(x,z), and the corresponding value of p(x,z,t)
at that location.
.The problem is that in this form, the x coordinate in the pressure
field is Fourier transformed and there is no direct
correspondence between a point in the medium of coordinates (x,z),
the velocity v(x,z), and the corresponding value of p(x,z,t)
at that location.
For a laterally invariant velocity and small values of dz, we can
consider the velocity constant for a thin depth interval. We write
| ![\begin{displaymath}
k_z={\pm {[{\omega^2 \over v^2}-{k^2_x }]^{1 \over 2}}}\end{displaymath}](img6.gif) |
(4) |
where kz is constant for two given values of kx and 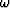 .Equation (3) becomes an ordinary differential equation
.Equation (3) becomes an ordinary differential equation
| 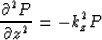 |
(5) |
which has the analytic solution
| 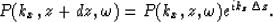 |
(6) |
Using equation (5) to downward extrapolate the wave field
in laterally invariant velocity media v(z) forms the basis of
the classic Phase Shift algorithm (Gazdag, 1978).
For laterally variant media, Gazdag (1984) proposes to downward
extrapolate the wave field one depth interval at a time with several
velocities, then to inverse Fourier transform in x the extrapolated field
and finally to interpolate each point along the X axis.
In other words starting with equation (3) we consider
several constant velocities (v1, v2, ...) in the interval
[vmin,vmax] and downward extrapolate the wavefield
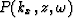 to
to 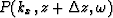 with
each velocity.
The resulting wavefields
with
each velocity.
The resulting wavefields
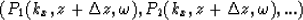
are then inverse Fourier transformed
in the direction of the X axis to obtain
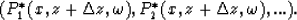
To obtain a single downward
extrapolated wavefield, for each point of X coordinates associated
with a velocity v(z,x), the value of the resulting wavefield
in this point is interpolated between the two wavefields with
closest velocities.
In addition to this idea, Gazdag (1984) implements a technique in the
PSPI algorithm to ensure that all the zero dips (corresponding to the
case kx=0) are downward continued without distortion. The technique
consists of multiplying the wavefield 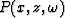 with
with
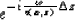
prior to the Fourier transformation
along the X axis and multiplying the downward extrapolated wavefield
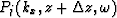 by
by
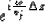
where
the subscript j denotes the index of the constant velocity used in the
downward extrapolation step.
As it will be seen later in the Split-step Fourier method, this supplemental
phase subtractieon and addition improves the accuracy of the results.





Next: THE SPLIT-STEP FOURIER METHOD
Up: Popovici : PSPI and
Previous: INTRODUCTION
Stanford Exploration Project
12/18/1997
![]()
![]() to
to ![]() with
each velocity.
The resulting wavefields
with
each velocity.
The resulting wavefields
![]()
![]()
![]() with
with
![]()
![]()