




Next: DEFINING AN IMAGING CRITERION
Up: IMAGING CONDITION
Previous: Scattering matrix coefficient
Most imaging methods described in the literature involve the correlation
between scalar wavefields. An exception is the tensorial imaging
condition formulated by Karrenbach (1991):
![\begin{displaymath}
\delta c_{jklm}(x,z,t) = \partial_m [\phi^s_l(x,z,t)] \partial_k
[\delta \phi^r_j(x,z,t)],\end{displaymath}](img19.gif)
where 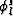 is the l component of the forward modeled shot wavefield,
and
is the l component of the forward modeled shot wavefield,
and 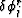 is the reverse propagated difference between the
forward modeled wavefield at the receivers and the recorded wavefield.
This process is equivalent to one step of a wavefield inversion scheme,
and
is the reverse propagated difference between the
forward modeled wavefield at the receivers and the recorded wavefield.
This process is equivalent to one step of a wavefield inversion scheme,
and 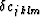 can be interpreted as the estimated perturbation
in the stiffness tensor. In this sense, it can be considered as an extension
of Tarantola's (1986) elastic inversion theory to the general anisotropic
case.
can be interpreted as the estimated perturbation
in the stiffness tensor. In this sense, it can be considered as an extension
of Tarantola's (1986) elastic inversion theory to the general anisotropic
case.
Hildebrand (1987) used a variation of this principle to image
for the acoustic impedance rather than the reflection coefficient, using
reverse-time migration to extrapolate the pressure and particle-velocity
wavefields. Contrary to the above formulation, Hildebrand's approach
obtained a image of the impedance (rather than perturbations), using
a recursive depth extrapolation procedure.





Next: DEFINING AN IMAGING CRITERION
Up: IMAGING CONDITION
Previous: Scattering matrix coefficient
Stanford Exploration Project
11/18/1997
![]()