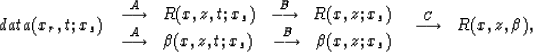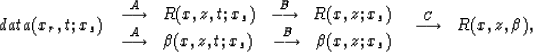Next: Correlation-based criterion
Up: Cunha: Reverse-time Migration
Previous: Stiffnesses perturbations
The imaging conditions discussed in the previous section obtain an estimation
of the imaging attribute at a particular point in the four-dimensional (for
a 2D treatment) 2D-space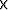 time
time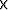 shot-position domain.
The imaging criterion defines the statistical approach involved to
reduce these information to the expectation value of the attribute in the
three-dimensional domain spanned by 2D-space
shot-position domain.
The imaging criterion defines the statistical approach involved to
reduce these information to the expectation value of the attribute in the
three-dimensional domain spanned by 2D-space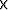 incidence-angle.
There are two major paths to perform this reduction
incidence-angle.
There are two major paths to perform this reduction
| 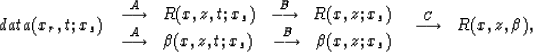 |
(7) |
or
| 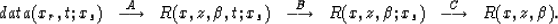 |
(8) |
In the first path A represents the depth extrapolation and imaging for time
t, B represents the time integration process and C represents the final
search over different shot-gathers to build the function 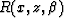 .In the second path A also represents the depth extrapolation and imaging
for time t, B represents the time integration process and C represents
the integration over the shot-point axis.
The first one starts with an independent estimation of the attribute and
the angle for each shotpoint, while the second obtains from
the beginning an estimation of the angular distribution of the attribute for
each shotpoint.
.In the second path A also represents the depth extrapolation and imaging
for time t, B represents the time integration process and C represents
the integration over the shot-point axis.
The first one starts with an independent estimation of the attribute and
the angle for each shotpoint, while the second obtains from
the beginning an estimation of the angular distribution of the attribute for
each shotpoint.





Next: Correlation-based criterion
Up: Cunha: Reverse-time Migration
Previous: Stiffnesses perturbations
Stanford Exploration Project
11/18/1997