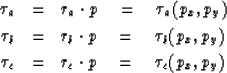
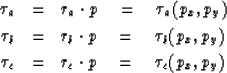 |
(1) | |
| (2) | ||
| (3) |
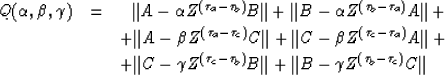 |
||
| (4) |
The value of (px,py) is found by the global search of Q(px,py).
A two-dimensional search on (px,py) space
is not as costly as it sounds.
We can first run burone() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) for each of the three rows in equation (4)
for all possible one-dimensional stepouts
and tabulate the outputs.
Then the two-dimensional global search
requires only a few additions from the tables
for each point in (px,py) space.
for each of the three rows in equation (4)
for all possible one-dimensional stepouts
and tabulate the outputs.
Then the two-dimensional global search
requires only a few additions from the tables
for each point in (px,py) space.
If we were to follow the philosophy of my 2-D code,
the value of the interpolated trace is far less
important than the fact
that we have used the (px,py) from above.
In other words, we can throw away
![]() .The value of the unknown trace could be
.The value of the unknown trace could be
| (5) |
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
There are many ways to bake the cake.
I believe, however, the most important feature
of any formulation is that it should
maintain a very minimal number of adjustable parameters
because we want to go to very small time gates.
If the original data were on a regular rectangular mesh,
instead of an arbitrary three locations,
then we can reduce the three free parameters above to two.
First, permit me to change variables so all the values of
![]() are unity.
Then use
are unity.
Then use ![]() for north-south correlation and
for north-south correlation and ![]() for
east-west correlation.
for
east-west correlation.
| (6) |