 |
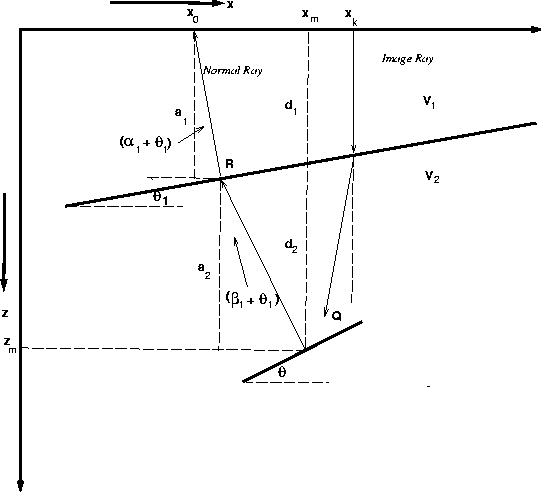
Figure 10 Geometry and raypaths for the dipping layer model. The diffractor is positioned at (xm,zm). The spatial and temporal coordinates of the diffraction curve and time migrated image are given by (x0,z0) and (xk,zk), respectively.
Black and Brzostowski 1993 derive simple expressions for the positioning error of time migration. We have used some of their intermediate results in equations(A-4)-(A-6) to calculate the theoretical plume response. In this section we review Black and Brzostowski's first-order theory of plumes and compare it to our previous results.
The geometry used for the derivation of the theoretical result is illustrated in Figure 10. Starting at the point diffractor location (xm,zm), a normal ray is traced to the surface where it emerges at x0. Time migration then translates us to the point xk. Black and Brzostowski go on from xk along the image ray to the point Q. The difference between Q and (xm,zm) is the error after the image ray correction. Since we are concerned with the response of time migration to lateral velocity variation, we are interested in the time migrated position (xk,tk).
 |
The velocity gradient which gives rise to the plumes is due to the velocity
contrast across the dipping layer and the dip angle ![]() .To simplify the analysis velocity contrast is defined as:
.To simplify the analysis velocity contrast is defined as:
![]()
| |
(4) |
| |
(5) |
| (6) |
By varying ![]() , equations(4) and (5) define a diffraction
curve like that given in Figure 2. The first term of the equations
yields the constant velocity hyperbola, the second term contains the effects
of vertical velocity gradients, the third and fourth terms contain the effects
of lateral velocity changes.
, equations(4) and (5) define a diffraction
curve like that given in Figure 2. The first term of the equations
yields the constant velocity hyperbola, the second term contains the effects
of vertical velocity gradients, the third and fourth terms contain the effects
of lateral velocity changes.
Time migration is carried out by performing the common-tangent construction.
Matching the slope of the hyperbola in equation (1) to the
time dip D of the event leads to equations(2) and (3).
Expanding these to first order in ![]() and
and ![]() gives the
spatial and temporal position of the event after time migration:Black and Brzostowski (1993).
gives the
spatial and temporal position of the event after time migration:Black and Brzostowski (1993).
| |
(7) |
| |
(8) |
We can vary ![]() in equations (7) and (8)
to get a first order analytic representation for the
plume. This is done for propagation angles of
in equations (7) and (8)
to get a first order analytic representation for the
plume. This is done for propagation angles of ![]() in
Figure 11.
in
Figure 11.
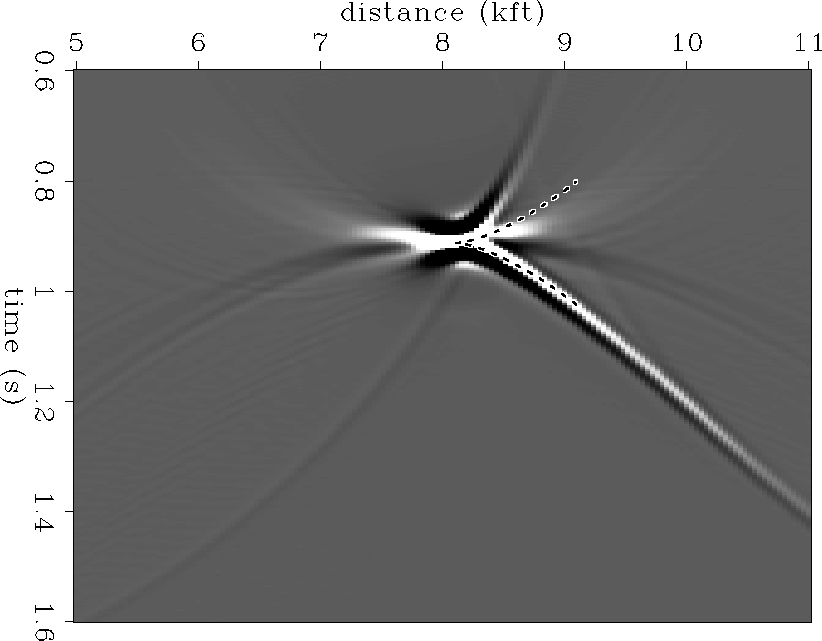
The theoretical result is well positioned relative to the synthetic result. The synthetic plume is skewed upwards whereas the theoretical plume is symmetric about a horizontal axis drawn through its apex. The lower limb of the theoretical plume overlies the synthetic result very closely, however the upper limbs do not match. Both the theoretical and synthetic plume open in the same direction and display the same type of limb curvature: convex upward on the upper limb and convex downward on the lower limb.
Although the first order theory contains some of the features of the plume, it is incomplete. It is clear that a higher-order theory is needed to explain all the features of time migration plumes.
 |