




Next: CONCLUSION
Up: Black et. al.: Plume
Previous: AGREEMENT WITH GEOMETRICAL CONSTRUCTION
The first-order theory of plume velocity dependence is developed here
following steps similar to Black and Brzostowski 1993 and
Paper 1.
We begin with the zero-offset time migration curve:
| ![\begin{displaymath}
{t_0^2} = {t_k^2} + 4{\left[{x_0 - x_k \over V_{mig}}\right]}^2\end{displaymath}](img7.gif) |
(3) |
Defining the velocity contrast across the dipping reflector in
Figure 6 as
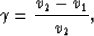
and the dip angle as 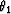 , Black and Brzostowski 1993
use the geometry of Figure 6
to express the true diffraction curve
to first order in
, Black and Brzostowski 1993
use the geometry of Figure 6
to express the true diffraction curve
to first order in 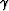 and
and 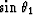 as:
as:
| 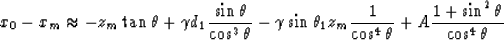 |
(4) |
| 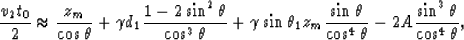 |
(5) |
where the quantity A is defined as
| 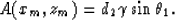 |
(6) |
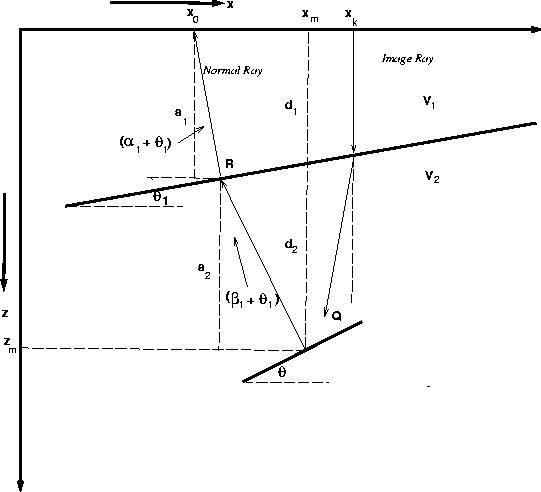
fig2
Figure 6 Geometry and raypaths for the dipping layer model. The diffractor is positioned
at (xm,zm). The spatial and temporal coordinates of the diffraction curve
and time migrated image are given by (x0,z0) and (xk,zk), respectively.

Matching the slope of the time migration curve
with the time dip D of the true diffraction curve leads to the following
formulas for the position of the time migrated point (xk,tk):
| ![\begin{displaymath}
x_k = x_0 - {\left[{V_{mig}D \over 2}\right] \left[{V_{mig}t_0 \over 2}\right]}
,\end{displaymath}](img15.gif) |
(7) |
| ![\begin{displaymath}
t_k = t_0 \sqrt {1 - {\left[{V_{mig}D \over 2}\right]}^2},\end{displaymath}](img16.gif) |
(8) |
where the time dip D
can be expressed
to first order in 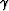 and
and 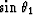 as:
as:
| 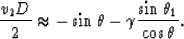 |
(9) |
Black and Brzostowski 1993 define the
RMS migration velocity V(xm,tm) at the correct migrated position
(xm,tm) to first-order in 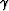 and
and 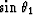 as:
as:
| ![\begin{displaymath}
\left[\frac{V(x_m,t_m)}{v_2}\right]^2 \approx 1-2\gamma\frac{d_1}{z_m}.\end{displaymath}](img18.gif) |
(10) |
Since we are interested in the variation of the plume operator with migration
velocity, we define
| 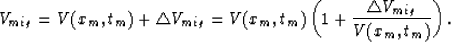 |
(11) |
Considering small values of 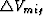 so that
so that
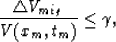
we can expand Vmig2 retaining only first-order terms as:
| 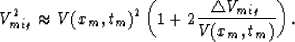 |
(12) |
We are finally ready to derive the first-order theory of plume velocity
dependence.
Time migration is carried out by inserting equations (4), (5),
(10), and (12) into equations (7) and
(8). Retaining only the terms which are first order in
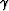 and
and 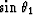 allows us to express
the first order theory for a perturbation in migration velocity
by the following equations:
allows us to express
the first order theory for a perturbation in migration velocity
by the following equations:
| 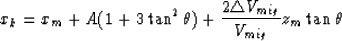 |
(13) |
| 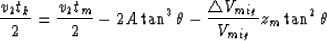 |
(14) |
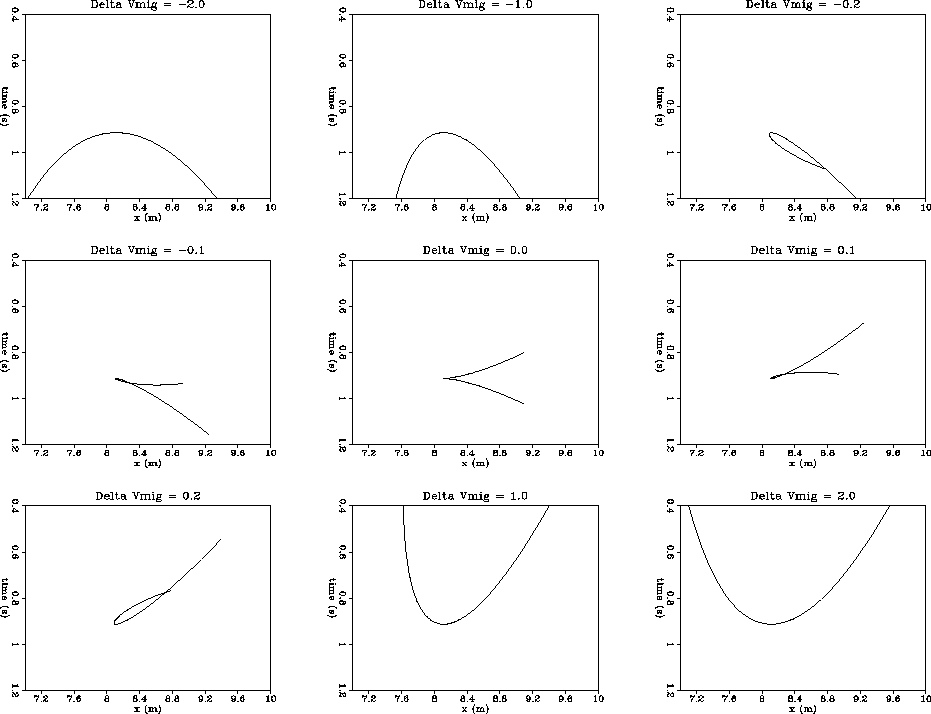
The theoretical curves given
by equations (13) and (14) are plotted in
Figure 7 for the same values of migration velocity that are used
in Figures 4 and 5.
Notice that if 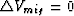 equations (13) and
(14) reduce to equations (1) and (2).
The center frame of Figure 7 (
equations (13) and
(14) reduce to equations (1) and (2).
The center frame of Figure 7 (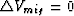 ) is generated
using the RMS well velocity. It is the same as the first-order
curve overlaid on the migration result in Figure 2.
) is generated
using the RMS well velocity. It is the same as the first-order
curve overlaid on the migration result in Figure 2.
theory
Figure 7 First-order theory of plume velocity dependence. The same migration velocities
used in Figures 4 and 5 are used here. The center frame Delta Vmig = 0.0
is generated using the RMS well velocity of 8.84 kft/s. It is the same
curve that is overlaid on Figure 2.





The first-order theory does not match the tangent construction
(Figure 5) and Kirchhoff migration (Figure 4) results
exactly; however,
we can qualitatively follow the plume formation in Figure 7 just as
we did in the other two cases. The curve progresses from an undermigrated
frown to an overmigrated smile as the migration velocity increases.
It is evident how the left limb of the frown curls around to form the upper
limb of the plume (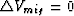 ) and later, as velocity increases
even more, into the right side of the smile. Similarly, the right limb
of the frown becomes the lower limb of the plume, and as velocity increases,
it becomes the left side of the smile. We do not observe the slight
clockwise rotation in the three middle frames with this simple first-order
theory.
) and later, as velocity increases
even more, into the right side of the smile. Similarly, the right limb
of the frown becomes the lower limb of the plume, and as velocity increases,
it becomes the left side of the smile. We do not observe the slight
clockwise rotation in the three middle frames with this simple first-order
theory.





Next: CONCLUSION
Up: Black et. al.: Plume
Previous: AGREEMENT WITH GEOMETRICAL CONSTRUCTION
Stanford Exploration Project
11/17/1997
![\begin{displaymath}
{t_0^2} = {t_k^2} + 4{\left[{x_0 - x_k \over V_{mig}}\right]}^2\end{displaymath}](img7.gif)
![\begin{displaymath}
{t_0^2} = {t_k^2} + 4{\left[{x_0 - x_k \over V_{mig}}\right]}^2\end{displaymath}](img7.gif)
![]()
![]() and
and ![]() as:
as:
![]()
![]() and
and ![]() allows us to express
the first order theory for a perturbation in migration velocity
by the following equations:
allows us to express
the first order theory for a perturbation in migration velocity
by the following equations:
![]() equations (13) and
(14) reduce to equations (1) and (2).
The center frame of Figure 7 (
equations (13) and
(14) reduce to equations (1) and (2).
The center frame of Figure 7 (![]() ) is generated
using the RMS well velocity. It is the same as the first-order
curve overlaid on the migration result in Figure 2.
) is generated
using the RMS well velocity. It is the same as the first-order
curve overlaid on the migration result in Figure 2.
![]() ) and later, as velocity increases
even more, into the right side of the smile. Similarly, the right limb
of the frown becomes the lower limb of the plume, and as velocity increases,
it becomes the left side of the smile. We do not observe the slight
clockwise rotation in the three middle frames with this simple first-order
theory.
) and later, as velocity increases
even more, into the right side of the smile. Similarly, the right limb
of the frown becomes the lower limb of the plume, and as velocity increases,
it becomes the left side of the smile. We do not observe the slight
clockwise rotation in the three middle frames with this simple first-order
theory.