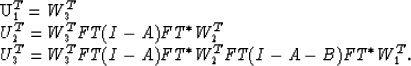Next: Examples
Up: Ji and Claerbout: Migration
Previous: Examples
In the first method, discussed in the previous section,
the wavefield is continuously propagated
to the top of the surface
after it is recorded at the lower altitude.
This is not physically possible
because after recording at the surface
the wavefield goes through air and
the air velocity is negligible compared to the earth velocity.
In order to make the modeling realistic,
we introduce a filter after each extrapolation
to stop the propagation of the wavefield after recording.
If the wavefield only has only vertical component,
the filter introduced has no special effect.
However, there is a significant difference
between examples with and without the filter
when the wavefield has large stepout.
The improved scheme by use of the filter
is explained schematically in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
tpmdlschm2
.
tpmdlschm2
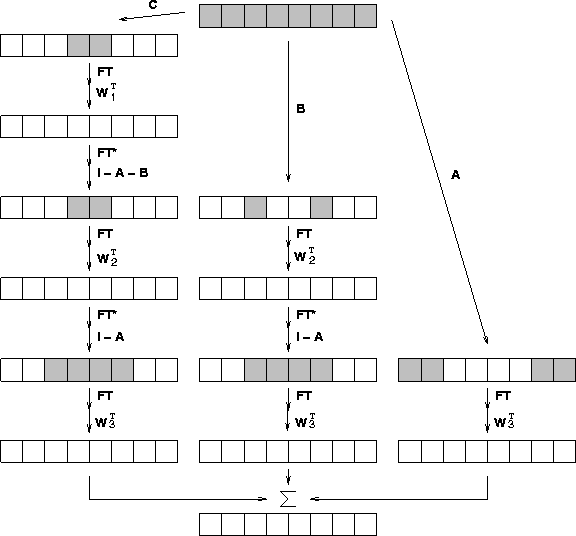
Figure 7 Modeling scheme 2 :
The schematic diagram for the wavefield extrapolation
when the surfaces are irregular with spatial filters that
stop the wavefield after recording.
Wj represents the upward propagating operator,
I is the identity matrix,
and A,B and C are matrices in equation (2).
[ Compare to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . ]
. ]

The scheme shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) can be algebraically formulated as
can be algebraically formulated as
| ![\begin{displaymath}
\left[
\begin{array}
{ccc}
A&B&C\end{array}\right]
\left[
\b...
...right]
=
\left[
\begin{array}
{c}
d_{surface}\end{array}\right]\end{displaymath}](img12.gif) |
(4) |
Now, the datuming operator can be found by
taking the conjugate transpose operator
of the modeling operator in equation (4).
Therefore, the improved datuming of the data gathered on an irregular
surface is done by
| ![\begin{displaymath}
\left[
\begin{array}
{ccc}
U_1^T&U_2^T&U_3^T\end{array}\righ...
...}\right]
=
\left[
\begin{array}
{c}
D_{datum}\end{array}\right]\end{displaymath}](img10.gif) |
(5) |
The schematic diagram of this datuming operator is given
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
tpmigschm2
Figure 8 Datuming scheme 2 :
Schematic diagram for datuming
when the surfaces are irregular as the conjugate operator
to the modeling scheme 2.
WjT represents the downward propagating operator.
[ Compare to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . ]
. ]






Next: Examples
Up: Ji and Claerbout: Migration
Previous: Examples
Stanford Exploration Project
11/17/1997
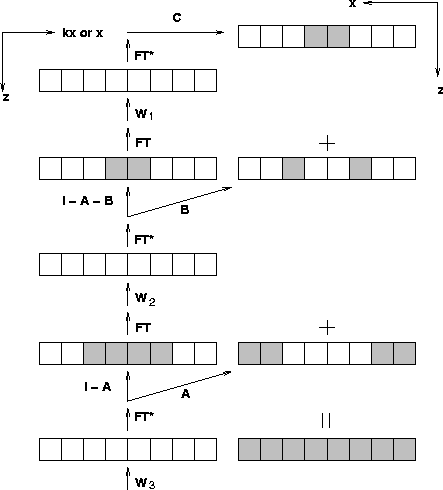
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . ]
. ]
![\begin{displaymath}
\left[
\begin{array}
{ccc}
A&B&C\end{array}\right]
\left[
\b...
...right]
=
\left[
\begin{array}
{c}
d_{surface}\end{array}\right]\end{displaymath}](img12.gif)
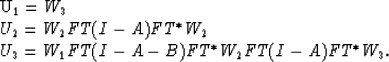
![\begin{displaymath}
\left[
\begin{array}
{ccc}
U_1^T&U_2^T&U_3^T\end{array}\righ...
...}\right]
=
\left[
\begin{array}
{c}
D_{datum}\end{array}\right]\end{displaymath}](img10.gif)