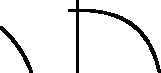Next: About this document ...
Up: Dellinger, Muir, & Karrenbach:
Previous: Acknowledgments
- Byun, B. S., Corrigan, D., and Gaiser, J. E., 1989,
Anisotropic velocity analysis for lithology discrimination:
Geophysics, 54, 1564-1574.
- Dellinger, J., and Muir. F., 1988,
Imaging reflections in elliptically anisotropic media:
Geophysics, 53, 1616-1618.
- Dellinger, J., 1991, Anisotropic seismic wave propagation:
Ph.D. thesis, Stanford University, Stanford, California, USA.
- Garmany, J., 1989, A student's garden of anisotropy:
Ann. Rev. Earth Planet. Sci., 17, 285-308.
- Gonzalez, A., Lynn, W., and Robinson, W.F. IV, 1991,
Prestack Frequency-Wavenumber (f-k) Migration in a Transversely Isotropic
Medium:
Expanded Abstracts of the 61st Annual International Meeting of the SEG,
1155-1157.
- Jones, E. A., and Wang, H. F., 1981,
Ultrasonic velocities in Cretaceous shales from the Williston basin:
Geophysics, 46, 288-297.
- Knuth, D. E., 1981,
The art of computer programming, volume 2: seminumerical algorithms:
Addison-Wesley, Reading, Massachussetts, USA.
- Schoenberg, M., and Muir, F., 1989, A calculus for finely
layered anisotropic media: Geophysics, 54, 581-589.
- Sena, A. G., 1991,
Seismic traveltime equations for azimuthally anisotropic and isotropic
media: Estimation of interval elastic properties:
Geophysics, 56, 2090-2101.
- Wolfram, S., 1988, Mathematica: A System for Doing Mathematics
by Computer: Addison-Wesley, Reading, Massachussetts, USA.
Group-four
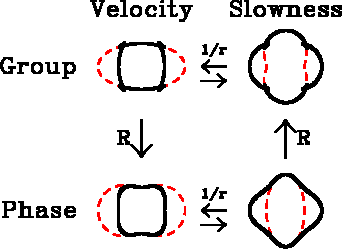
Figure 1
Plots of group velocity (impulse response), group slowness, phase velocity,
and phase slowness (dispersion relation) for the qSV mode of
Greenhorn Shale (thick solid line) and the elliptically anisotropic
vertical-paraxial approximation (thin dashed line).
The four plots are connected by only two transformations,
here labeled ``1/r'' and ``R''.
The transformation ``1/r'' (invert the radial coordinate)
is its own inverse, as is the combined transformation
``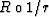 '' that goes from group velocity
to phase slowness (and vice versa). The
combined transformation also maps ellipses onto ellipses.
(Garmany, 1989) and (Dellinger, 1991)
'' that goes from group velocity
to phase slowness (and vice versa). The
combined transformation also maps ellipses onto ellipses.
(Garmany, 1989) and (Dellinger, 1991)
 Sample
Sample
Figure 2
The curves that result for three different values of the F factor
in equation (10); the asterisks mark the origin.
On the left, F = 3/7; in the middle F = 1 and the curve is
an ellipse; on the right F = 7/3.
 Compare.s.1
Compare.s.1
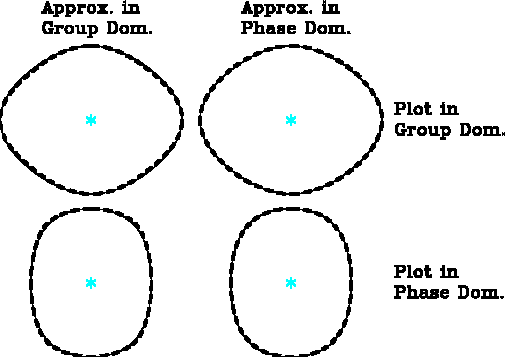
Figure 3
Group-velocity and phase-slowness plots of the qP surface of
Greenhorn shale (thin solid line) and the corresponding
first anelliptic approximation (thick dashed line).
On the left the approximation is made in the group-velocity domain;
on the right the approximation is made in the phase-slowness domain.
The approximations are consistent to within about two percent.
 Compare.s.-1
Compare.s.-1
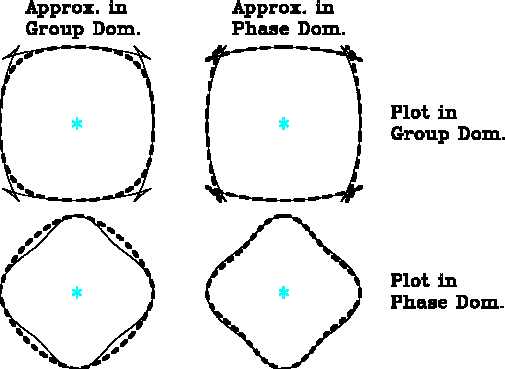
Figure 4
As in Figure 3, but for the considerably more
anisotropic qSV surface.
The approximations in the two domains are not consistent around
the triplication.
 perfect
perfect
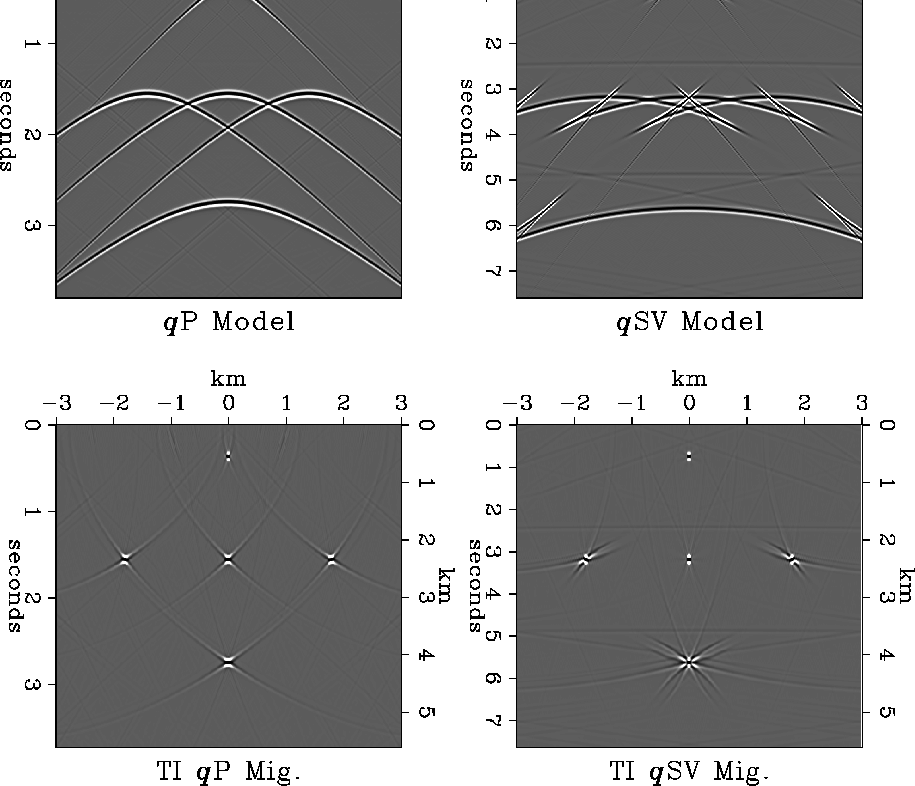
Figure 5
Scalar Stolt modeling and migration for qP and qSV
waves in a TI medium.
(W11=13.72,
W13=4.28,
W33=9.08,
W44=2.16, and
W66=4.24, all in km/s.)
Top: qP and qSV models resulting
from four point reflectors arranged in a diamond-shaped lattice.
Bottom: Exact Stolt migrations of the modeled data.
The hyperboloids do not completely collapse back to
points because of the truncations at the model edges.
 approxI
approxI
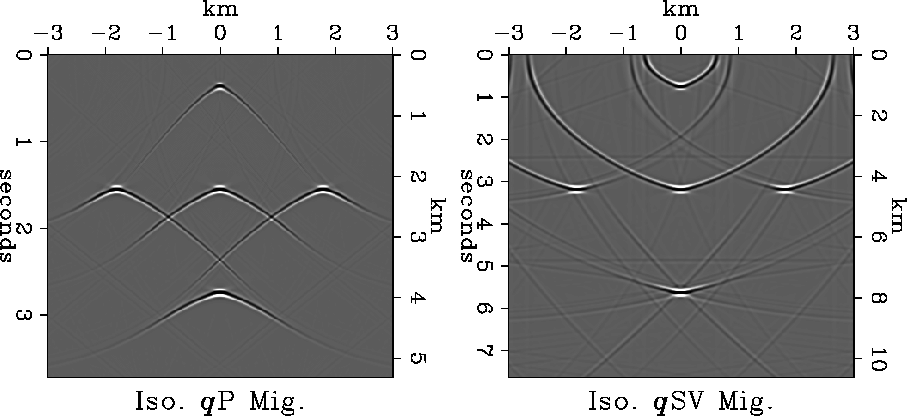
Figure 6
Approximate isotropic migrations
of the exact TI models in Figure 5.
The P migration velocity (left) was
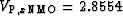 km/s;
the S migration velocity (right) was
km/s;
the S migration velocity (right) was
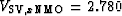 km/s.
km/s.
 approxA1
approxA1
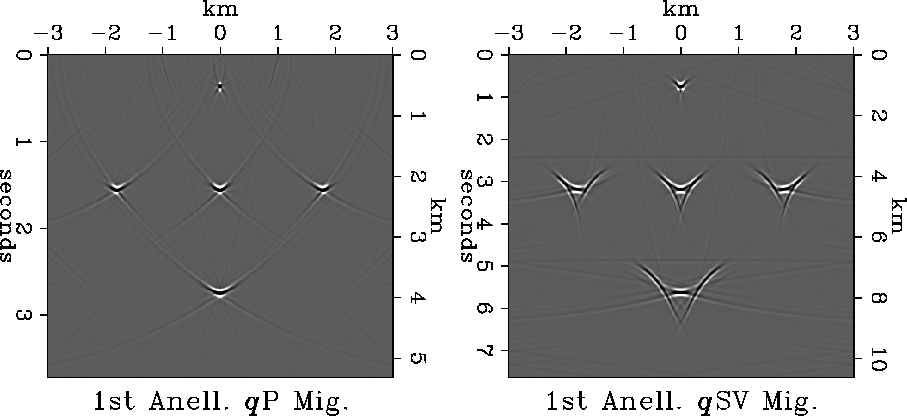
Figure 7
Approximate migrations of the exact TI models
in Figure 5 using the first anelliptic approximation.
For the qP waves, the migration used
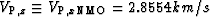 ,and
,and 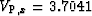 km/s.
For the qSV waves, the migration used
km/s.
For the qSV waves, the migration used
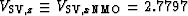 km/s,
and
km/s,
and 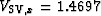 km/s.
(The unconstrained vertical velocities are set equal to the moveout
velocities to conform to the usual practice; the vertical scale thus
chosen has no effect on the time migration.)
km/s.
(The unconstrained vertical velocities are set equal to the moveout
velocities to conform to the usual practice; the vertical scale thus
chosen has no effect on the time migration.)
 approxA2
approxA2
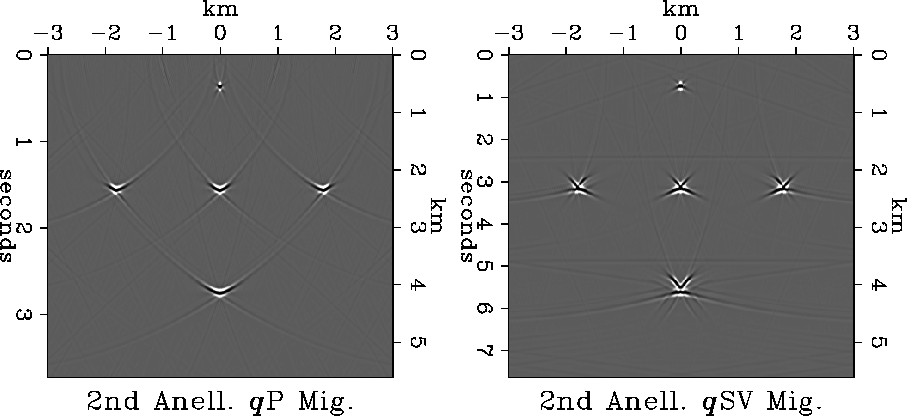
Figure 8
Approximate migrations of the exact TI models
in Figure 5 using the second anelliptic approximation.
For the qP waves, the migration used
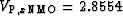 km/s,
km/s,
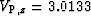 km/s,
km/s,
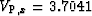 km/s, and
km/s, and
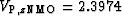 km/s.
For the qSV waves, the migration used
km/s.
For the qSV waves, the migration used
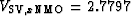 km/s,
km/s,
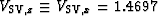 km/s
(from the symmetry of TI), and
km/s
(from the symmetry of TI), and
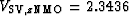 km/s.
In this migration the vertical scale is assumed to be known.
km/s.
In this migration the vertical scale is assumed to be known.
 NMOfig
NMOfig
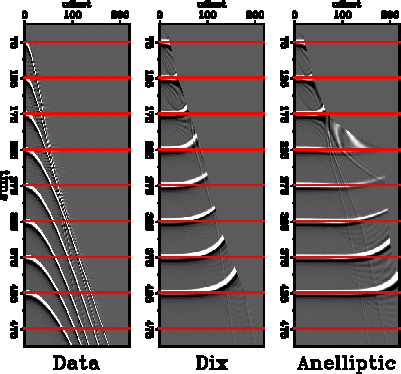
Figure 9
Anelliptic moveout removal.
The model consists of 8 layers and a halfspace,
the top layer 75 time-units thick and all others
50 time-units thick.
The layer moveout velocities from top to bottom are
.25, .3, .4, .45, .3, .3, .45, and .5.
(Units are arbitrary.)
All layers but the one from time 175 to 225 are isotropic.
The single anisotropic layer, fourth down,
corresponds to the qSV mode for elastic parameters
W11=.81,
W13=.3645,
W33=.8505,
and
W55=.243.
(The qSV moveout velocity is .45.)






Next: About this document ...
Up: Dellinger, Muir, & Karrenbach:
Previous: Acknowledgments
Stanford Exploration Project
11/17/1997