




Next: Elastic medium
Up: Karrenbach: Wave equation modules
Previous: Introduction
The general modeling implementation is based on a wave equation of the form
| 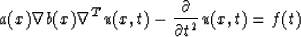 |
(1) |
u is an arbitrary wave field (scalar or vector); f is the force applied
at a source location. 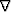 is a gradient and
is a gradient and 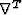 the divergence operator applied to the wavefield components.
a and b are medium property fields (density, velocity or stiffnesses).
Equation (1) can be rewritten as a sequence of first order
partial differential equations. Numerical calculations typically use those
on a staggered grid for improved accuracy.
the divergence operator applied to the wavefield components.
a and b are medium property fields (density, velocity or stiffnesses).
Equation (1) can be rewritten as a sequence of first order
partial differential equations. Numerical calculations typically use those
on a staggered grid for improved accuracy.





Next: Elastic medium
Up: Karrenbach: Wave equation modules
Previous: Introduction
Stanford Exploration Project
11/17/1997