ABSTRACT
The application of McClellan transformations considerably reduces the
computational cost of 3-D wavefield depth extrapolation
by explicit convolutional methods.
The accuracy of migration methods based on McClellan transformation depends
on how well the transformation filter (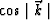 ) is approximated;
errors in this approximation cause anisotropy
in the extrapolator operator. This anisotropy can be greatly
reduced by rotating the approximate filter by 45 degrees,
and averaging the rotated filter with the original filter.
The application of the rotated filter yields a migration
method that images correctly very steep dips,
without additional computational cost. ) is approximated;
errors in this approximation cause anisotropy
in the extrapolator operator. This anisotropy can be greatly
reduced by rotating the approximate filter by 45 degrees,
and averaging the rotated filter with the original filter.
The application of the rotated filter yields a migration
method that images correctly very steep dips,
without additional computational cost.
|
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)