




Next: RESULTS OF 3-D POSTSTACK
Up: Biondi and Palacharla: 3-D
Previous: Introduction
The McClellan filters proposed by Hale 1991 to approximate
the 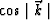 filter have the important advantage of being compact,
and consequently inexpensive to apply as convolutions in
space domain. The lower-order filter is applied
by convolving the data with a 9-point stencil, while
the higher-order one by convolving the data with a 17-point stencil.
However, both filters have an anisotropic
impulse response; that is,
their spectra vary with azimuth.
They fit very well the desired circular
spectrum of
filter have the important advantage of being compact,
and consequently inexpensive to apply as convolutions in
space domain. The lower-order filter is applied
by convolving the data with a 9-point stencil, while
the higher-order one by convolving the data with a 17-point stencil.
However, both filters have an anisotropic
impulse response; that is,
their spectra vary with azimuth.
They fit very well the desired circular
spectrum of 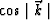 along the axes,
but differ from it at high wavenumbers.
The error is dependent on the azimuthal direction and
is maximum for azimuths rotated 45 degrees with respect to
the axes.
In this section we derive a filter that
is more isotropic than either of the McClellan filters
and has a computational cost comparable to the 17-point one.
The new filter is obtained by averaging the 9-point McClellan filter
with a 45 degrees rotated version of itself.
along the axes,
but differ from it at high wavenumbers.
The error is dependent on the azimuthal direction and
is maximum for azimuths rotated 45 degrees with respect to
the axes.
In this section we derive a filter that
is more isotropic than either of the McClellan filters
and has a computational cost comparable to the 17-point one.
The new filter is obtained by averaging the 9-point McClellan filter
with a 45 degrees rotated version of itself.
The representation of the 9-point McClellan filter in
the wavenumber domain is
| 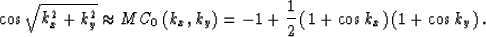 |
(1) |
In the wavenumber domain,
this filter can be easily rotated by an angle 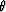 by applying the change of variables,
by applying the change of variables,
| 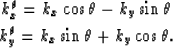 |
|
| (2) |
Applying this rotation to the McClellan filter we obtain the general
expression for a filter aligned with an azimuth rotated by 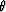 with respect to the axes,
with respect to the axes,
| ![\begin{eqnarray}
\lefteqn{ MC_{\theta}\left(k_x,k_y; \theta \right)= }
\nonumber...
...ht]\left[1+\cos\left(k_x\sin \theta+ k_y\cos \theta\right)\right].\end{eqnarray}](img9.gif) |
|
| (3) |
For an arbitrary 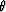 this filter cannot be approximated in the
space domain with a compact convolutional operator,
but in the special case of
this filter cannot be approximated in the
space domain with a compact convolutional operator,
but in the special case of 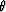 being equal
to 45 degrees, the general expression of equation (3)
simplifies to
being equal
to 45 degrees, the general expression of equation (3)
simplifies to
| ![\begin{displaymath}
MC_{45}\left(k_x,k_y; \theta=45^{\circ}\right)= -1+{1\over{2...
...}}}\right)+ \cos\left({k_y\over{\sqrt{2}}}\right)\right] }^{2}.\end{displaymath}](img10.gif) |
(4) |
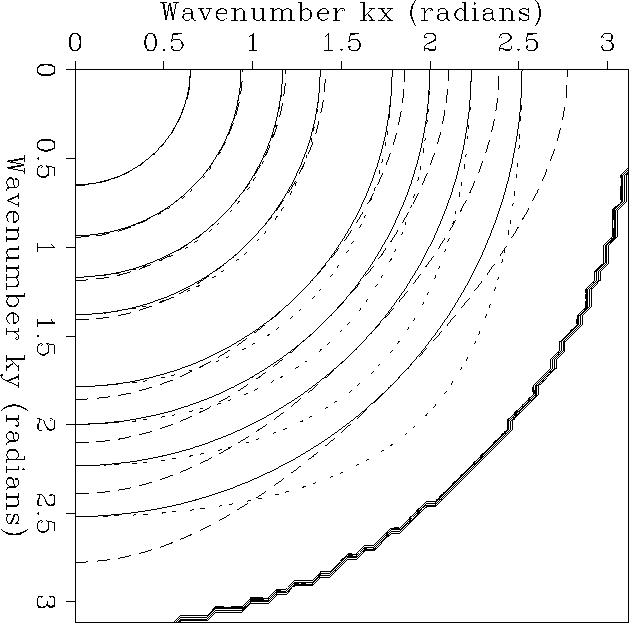
The spectrum of the the rotated operator is shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
As expected, it is the rotation of the
spectrum of the 9-point McClellan filter (dotted line).
The spectrum of the rotated filter matches the spectrum of
the desired filter (solid line) along the diagonals, but not
along the axes.
Before averaging the two filters we scale the
rotated filter such that it
matches
.
As expected, it is the rotation of the
spectrum of the 9-point McClellan filter (dotted line).
The spectrum of the rotated filter matches the spectrum of
the desired filter (solid line) along the diagonals, but not
along the axes.
Before averaging the two filters we scale the
rotated filter such that it
matches 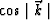 along the axes.
This scaling is a non-linear stretch of the wavenumbers axes,
that is defined by the relationships
along the axes.
This scaling is a non-linear stretch of the wavenumbers axes,
that is defined by the relationships
| ![\begin{eqnarray}
& \cos \overline{k_x}= -1+{1\over{2}}{\left[ \cos\left({k_x\ove...
...2}}{\left[ \cos\left({k_y\over{\sqrt{2}}}\right)+ 1 \right] }^{2},\end{eqnarray}](img11.gif) |
|
| (5) |
where the bars indicate that the wavenumber axes have
been remapped.
Solving for 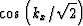 and
and 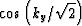 in
equation (5) leads to the relationships
in
equation (5) leads to the relationships
| 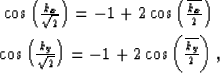 |
|
| (6) |
which upon substitution in
equation (4)
yield the desired filter
| ![\begin{displaymath}
\overline{{MC}_{45}}\left(\overline{k_x},\overline{k_y}\righ...
...ht)+ \cos\left({\overline{k_y}\over{2}}\right)-1 \right] }^{2}.\end{displaymath}](img15.gif) |
(7) |
rot
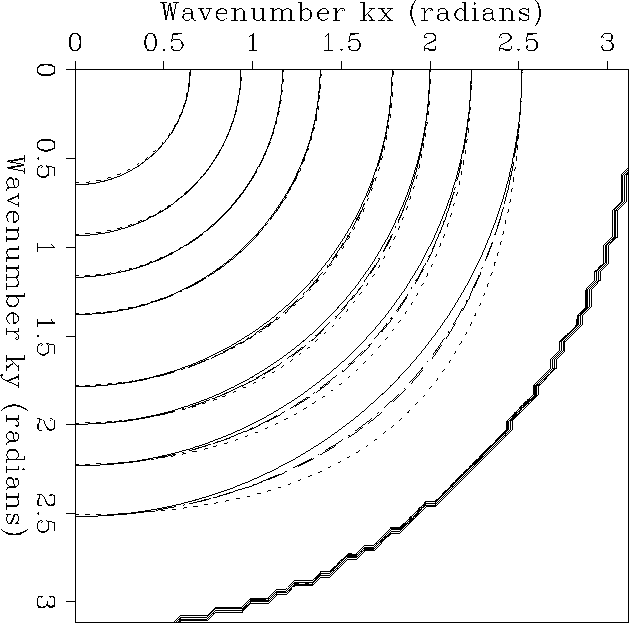
Figure 1 Contours of constant amplitude for the spectra of the 9-point McClellan
transformation filter (double dots), the 45 degree rotate 9-point McClellan
filter (dash) and the ideal
circularly symmetric filter (solid).





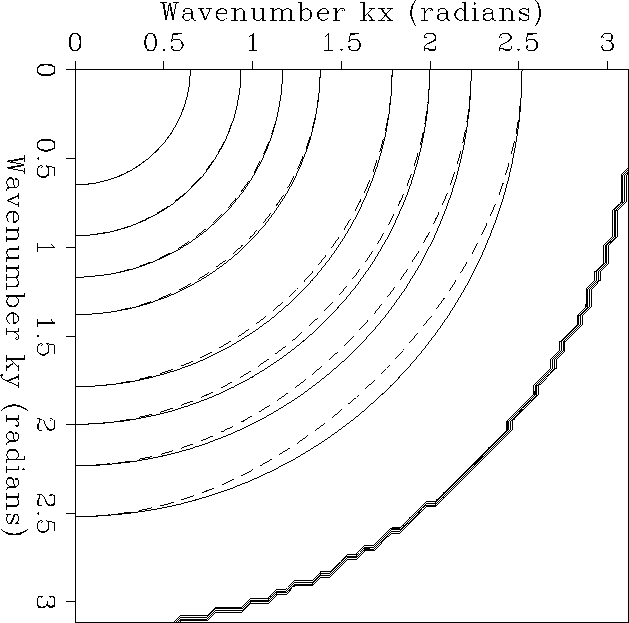
The spectrum of the new operator is shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with a dashed line.
As expected, it matches the spectrum of
with a dashed line.
As expected, it matches the spectrum of 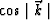 along the axes, but not along the diagonals.
However, the arithmetic and the geometric
averages of the original 9-point McClellan filter
along the axes, but not along the diagonals.
However, the arithmetic and the geometric
averages of the original 9-point McClellan filter 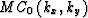 with
the newly derived rotated filter
with
the newly derived rotated filter 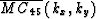 are filters with almost isotropic spectrum.
Figure
are filters with almost isotropic spectrum.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the spectrum of the averaged filters
(dot dash for the arithmetic average and double dash
for the geometric average)
compared with the ideal filter (solid line) and the 17-point
McClellan filter proposed by Hale (fine dash).
The spectra of the averaged filters are similar and both match exactly
the ideal spectrum along the axis and deviate from it
considerably less than the spectrum of the 17-point McClellan
filter across the whole range of azimuths.
shows the spectrum of the averaged filters
(dot dash for the arithmetic average and double dash
for the geometric average)
compared with the ideal filter (solid line) and the 17-point
McClellan filter proposed by Hale (fine dash).
The spectra of the averaged filters are similar and both match exactly
the ideal spectrum along the axis and deviate from it
considerably less than the spectrum of the 17-point McClellan
filter across the whole range of azimuths.
rotscal
Figure 2 Contours of constant amplitude for the spectra of the
scaled McClellan (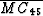 transformation filter (dash) and the ideal
circularly symmetric filter (solid).
transformation filter (dash) and the ideal
circularly symmetric filter (solid).





The filter 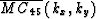 can be efficiently applied to the data
because the operator
can be efficiently applied to the data
because the operator
![${\left[ \cos\left({k_x/2}\right)+ \cos\left({k_y/2}\right)-1 \right) }]$](img19.gif) is separable;
its space-domain representation is a cross-shaped convolutional operator.
The arms of the cross are the space-domain representation of the
is separable;
its space-domain representation is a cross-shaped convolutional operator.
The arms of the cross are the space-domain representation of the
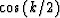 operator.
This filter can be approximated in different ways;
for computing the migration examples shown in the next section
we windowed its ideal impulse response with a 7-point
Kaiser window Oppenheim and Shafer (1975).
Consequently, to apply
operator.
This filter can be approximated in different ways;
for computing the migration examples shown in the next section
we windowed its ideal impulse response with a 7-point
Kaiser window Oppenheim and Shafer (1975).
Consequently, to apply 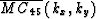 we convolved the data twice
with a 13-point cross;
longer filters can be used if more accuracy is required.
we convolved the data twice
with a 13-point cross;
longer filters can be used if more accuracy is required.
avg
Figure 3 Contours of constant amplitude for spectra of the 17-point modified McClellan
filter (double dots), the arithmetic averaged filter (dot dash), the
geometric averaged filter (double dash) and the ideal
circularly symmetric filter (solid).





The application of the arithmetic averaged filter requires
a convolution with the 9-point McClellan filter followed
by two convolutions with a 13-point cross.
The total cost of this operation is higher than convolving
the data
with the 17-point McClellan filter; though it yields more accurate results.
However, the geometric average is as close to the ideal filter
as the arithmetic average, and thus a very good approximation
is also achieved by applying 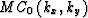 and
and 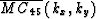 alternately
between depth steps.
The total computational cost of this procedure is
about the same as applying the 17-point McClellan filter.
alternately
between depth steps.
The total computational cost of this procedure is
about the same as applying the 17-point McClellan filter.





Next: RESULTS OF 3-D POSTSTACK
Up: Biondi and Palacharla: 3-D
Previous: Introduction
Stanford Exploration Project
11/17/1997
![]() filter have the important advantage of being compact,
and consequently inexpensive to apply as convolutions in
space domain. The lower-order filter is applied
by convolving the data with a 9-point stencil, while
the higher-order one by convolving the data with a 17-point stencil.
However, both filters have an anisotropic
impulse response; that is,
their spectra vary with azimuth.
They fit very well the desired circular
spectrum of
filter have the important advantage of being compact,
and consequently inexpensive to apply as convolutions in
space domain. The lower-order filter is applied
by convolving the data with a 9-point stencil, while
the higher-order one by convolving the data with a 17-point stencil.
However, both filters have an anisotropic
impulse response; that is,
their spectra vary with azimuth.
They fit very well the desired circular
spectrum of ![]() along the axes,
but differ from it at high wavenumbers.
The error is dependent on the azimuthal direction and
is maximum for azimuths rotated 45 degrees with respect to
the axes.
In this section we derive a filter that
is more isotropic than either of the McClellan filters
and has a computational cost comparable to the 17-point one.
The new filter is obtained by averaging the 9-point McClellan filter
with a 45 degrees rotated version of itself.
along the axes,
but differ from it at high wavenumbers.
The error is dependent on the azimuthal direction and
is maximum for azimuths rotated 45 degrees with respect to
the axes.
In this section we derive a filter that
is more isotropic than either of the McClellan filters
and has a computational cost comparable to the 17-point one.
The new filter is obtained by averaging the 9-point McClellan filter
with a 45 degrees rotated version of itself.
![]() by applying the change of variables,
by applying the change of variables,
![]() this filter cannot be approximated in the
space domain with a compact convolutional operator,
but in the special case of
this filter cannot be approximated in the
space domain with a compact convolutional operator,
but in the special case of ![]() being equal
to 45 degrees, the general expression of equation (3)
simplifies to
being equal
to 45 degrees, the general expression of equation (3)
simplifies to
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
As expected, it is the rotation of the
spectrum of the 9-point McClellan filter (dotted line).
The spectrum of the rotated filter matches the spectrum of
the desired filter (solid line) along the diagonals, but not
along the axes.
Before averaging the two filters we scale the
rotated filter such that it
matches
.
As expected, it is the rotation of the
spectrum of the 9-point McClellan filter (dotted line).
The spectrum of the rotated filter matches the spectrum of
the desired filter (solid line) along the diagonals, but not
along the axes.
Before averaging the two filters we scale the
rotated filter such that it
matches ![]() along the axes.
This scaling is a non-linear stretch of the wavenumbers axes,
that is defined by the relationships
along the axes.
This scaling is a non-linear stretch of the wavenumbers axes,
that is defined by the relationships
![\begin{eqnarray}
& \cos \overline{k_x}= -1+{1\over{2}}{\left[ \cos\left({k_x\ove...
...2}}{\left[ \cos\left({k_y\over{\sqrt{2}}}\right)+ 1 \right] }^{2},\end{eqnarray}](img11.gif)
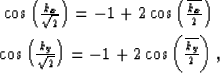
![\begin{displaymath}
\overline{{MC}_{45}}\left(\overline{k_x},\overline{k_y}\righ...
...ht)+ \cos\left({\overline{k_y}\over{2}}\right)-1 \right] }^{2}.\end{displaymath}](img15.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with a dashed line.
As expected, it matches the spectrum of
with a dashed line.
As expected, it matches the spectrum of ![]() along the axes, but not along the diagonals.
However, the arithmetic and the geometric
averages of the original 9-point McClellan filter
along the axes, but not along the diagonals.
However, the arithmetic and the geometric
averages of the original 9-point McClellan filter ![]() with
the newly derived rotated filter
with
the newly derived rotated filter ![]() are filters with almost isotropic spectrum.
Figure
are filters with almost isotropic spectrum.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the spectrum of the averaged filters
(dot dash for the arithmetic average and double dash
for the geometric average)
compared with the ideal filter (solid line) and the 17-point
McClellan filter proposed by Hale (fine dash).
The spectra of the averaged filters are similar and both match exactly
the ideal spectrum along the axis and deviate from it
considerably less than the spectrum of the 17-point McClellan
filter across the whole range of azimuths.
shows the spectrum of the averaged filters
(dot dash for the arithmetic average and double dash
for the geometric average)
compared with the ideal filter (solid line) and the 17-point
McClellan filter proposed by Hale (fine dash).
The spectra of the averaged filters are similar and both match exactly
the ideal spectrum along the axis and deviate from it
considerably less than the spectrum of the 17-point McClellan
filter across the whole range of azimuths.
![]() can be efficiently applied to the data
because the operator
can be efficiently applied to the data
because the operator
![]() is separable;
its space-domain representation is a cross-shaped convolutional operator.
The arms of the cross are the space-domain representation of the
is separable;
its space-domain representation is a cross-shaped convolutional operator.
The arms of the cross are the space-domain representation of the
![]() operator.
This filter can be approximated in different ways;
for computing the migration examples shown in the next section
we windowed its ideal impulse response with a 7-point
Kaiser window Oppenheim and Shafer (1975).
Consequently, to apply
operator.
This filter can be approximated in different ways;
for computing the migration examples shown in the next section
we windowed its ideal impulse response with a 7-point
Kaiser window Oppenheim and Shafer (1975).
Consequently, to apply ![]() we convolved the data twice
with a 13-point cross;
longer filters can be used if more accuracy is required.
we convolved the data twice
with a 13-point cross;
longer filters can be used if more accuracy is required.
![]() and
and ![]() alternately
between depth steps.
The total computational cost of this procedure is
about the same as applying the 17-point McClellan filter.
alternately
between depth steps.
The total computational cost of this procedure is
about the same as applying the 17-point McClellan filter.