The simplest extension to the phase shift algorithm is ``phase shift
plus interpolation'' (PSPI) Gazdag and Sguazzero (1984). This algorithm
approximates the extrapolation of the wavefield in a spatially varying
velocity field by interpolating the results of a set of constant
velocity extrapolations. The interpolation is performed in the space
domain. This method therefore requires an inverse Fourier transform of each
constant velocity panel back to the space domain (x or ![]() ), and
a forward transform of the interpolated result to the wavenumber domain,
for each extrapolation step in z or r.
), and
a forward transform of the interpolated result to the wavenumber domain,
for each extrapolation step in z or r.
I use the simplest form of the PSPI algorithm which uses only two constant velocity extrapolations. The two velocities are the maximum and minimum velocity at the current depth or radius.
In rectangular coordinates,
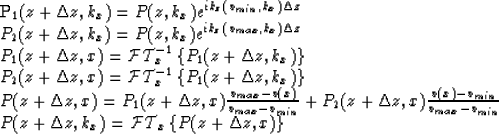 |
||
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the results of modeling in a medium which has a
linear gradient in x and z. The velocity field in this model is
shows the results of modeling in a medium which has a
linear gradient in x and z. The velocity field in this model is ![]() The plot on the left is computed in a
rectangular coordinates and the one on the right in polar coordinates. They
both show an asymmetric wavefront produced by the velocity gradient
The polar coordinate result contains
energy at higher dips that the rectangular coordinate result because it does
not start with a dip filtered impulse.
The plot on the left is computed in a
rectangular coordinates and the one on the right in polar coordinates. They
both show an asymmetric wavefront produced by the velocity gradient
The polar coordinate result contains
energy at higher dips that the rectangular coordinate result because it does
not start with a dip filtered impulse.
 |