Paraxial approximations

The most common way of extrapolating the wavefield in a variable velocity medium is to use a paraxial approximation to the wave equation. The well known $45^\circ$ paraxial approximation to equation (1) is,

$$\frac{\partial P} {\partial z } = i\frac{\omega}{v} P - \fra... ...1 + \frac{v^2}{4 \omega^2} \frac{\partial^2}{\partial x^2 }} P$$

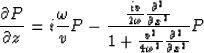
Using the usual splitting procedure this becomes,

$$(1 - \frac{v^2}{4 \omega^2}\frac{\partial^2}{\partial x^2 } ... ... z } = \frac{i v}{2 \omega} \frac{\partial^2 Q }{\partial x^2 }$$

followed by,

$$P(z+\Delta z) = exp( i \int \frac{\omega}{v} \Delta z ) Q(z+\Delta z).$$

Discretization of the first equation using the Crank-Nicholson scheme results in a tridiagonal set of equations to be solved in order to propagate the wavefield from a level z to $z+\Delta z$.

The equations in polar coordinates can be similarly transformed, the paraxial approximation is,

$$\frac{\partial P} {\partial r } =\left( \frac{-1}{r^2} + i \... ... \frac{\alpha}{4r^2} \frac{\partial^2}{\partial \theta^2 } } P$$

where,

$$\alpha = \sqrt{ \frac{\omega^2}{v^2} - \frac{1}{4r^2} }$$

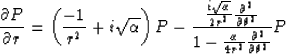
After splitting this becomes,

$$(1 - \frac{\alpha}{4r^2}\frac{\partial^2}{\partial \theta^2 ... ...\sqrt{ \alpha }}{2r^2} \frac{\partial^2 Q }{\partial \theta^2 }$$

followed by,

$$P(r+\Delta r ) = exp \left( \frac{-1}{r^2} + i \sqrt{ \alpha } \Delta r \right) Q(r+\Delta r)$$

Again discretization of the first equation yields a tridiagonal set of equations to be solved for each depth step.

The results of using these two schemes in a constant velocity space are shown in figure . The $45^\circ$ approximation is clearly visible in the rectangular coordinate data. Because the wavefront propagates at zero degrees to the polar coordinate frame, the polar data does not show any artifacts due to the $45^\circ$ approximation.

 

parax-both
Figure 6 Modeling in a constant velocity medium using the $45^\circ$ paraxial approximation. The plot on the left was computed in rectangular coordinates the plot on the right was computed in a polar coordinate frame.

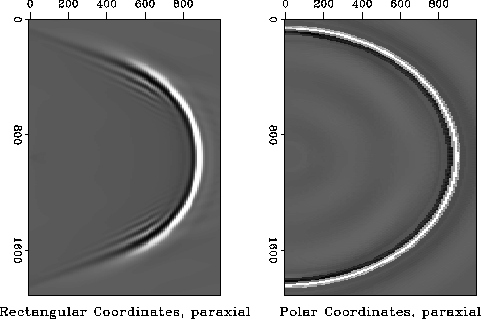Paraxial approximations will not accurately model events that propagate at high angles to the coordinate frame of the finite difference mesh. In rectangular coordinates this means that near vertical waves should be propagated using depth extrapolation, and near horizontal waves would be best modeled using x-extrapolation. If the problem to be solved is one of downward continuing surface data that contains events that are mostly near vertical (e.g. zero offset migration), a rectangular coordinate frame and depth extrapolation are appropriate. On the other hand if the problem is one of modeling a near circular outgoing wavefront from a point source, then polar coordinates and outward radial extrapolation are superior.