To begin, I define a forward model for a ``generalized'' PP reflectivity,
![]() , which combines elements of Zoeppritz plane wave reflection
(e.g., Aki and Richards, 1980),
and Rayleigh-Sommerfeld diffraction (e.g., Goodman, 1968).
I define a differential volume element
, which combines elements of Zoeppritz plane wave reflection
(e.g., Aki and Richards, 1980),
and Rayleigh-Sommerfeld diffraction (e.g., Goodman, 1968).
I define a differential volume element ![]() as
as
| |
(1) |
for ![]() , and zero otherwise.
Here, w is angular frequency,
, and zero otherwise.
Here, w is angular frequency, ![]() is compressional velocity,
is compressional velocity,
![]() is the Zoeppritz PP plane wave reflection coefficient
and
is the Zoeppritz PP plane wave reflection coefficient
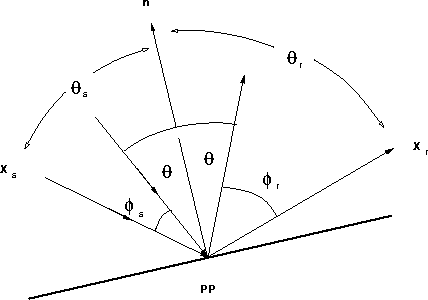
and ![]() (
(![]() ) is the
angle between the incident source (receiver) ray and the specular
ray in Figure
) is the
angle between the incident source (receiver) ray and the specular
ray in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The specular ray is defined as the reflection
raypath for which the incident angle
. The specular ray is defined as the reflection
raypath for which the incident angle ![]() is equal to the angle of
reflection, with respect to the normal to the reflecting surface.
The specular angle
is equal to the angle of
reflection, with respect to the normal to the reflecting surface.
The specular angle ![]() is related to
is related to ![]() and
and ![]() in that
in that
![]() , where
, where ![]() is
the angle between an arbitrary source ray and the reflector normal, and
is
the angle between an arbitrary source ray and the reflector normal, and
![]() is the angle between an arbitrary receiver ray and the reflector
normal. Frazer and Sen (1985, eqn. 9b) derive an analogous
expression to (1) for elastic Kirchhoff-Helmholtz surface integrals.
is the angle between an arbitrary receiver ray and the reflector
normal. Frazer and Sen (1985, eqn. 9b) derive an analogous
expression to (1) for elastic Kirchhoff-Helmholtz surface integrals.
 |
Equation (1) can be integrated over the subsurface volume to forward model the reflected scalar wavefield:
| |
(2) |
where ![]() (
(![]() ) is the shot (receiver) coordinate, and
) is the shot (receiver) coordinate, and ![]() is
the total traveltime from source to reflection point to receiver.
As (Ar)
is the WKBJ amplitude factor along the source (receiver) leg of the
raypath to the subsurface reflection point
is
the total traveltime from source to reflection point to receiver.
As (Ar)
is the WKBJ amplitude factor along the source (receiver) leg of the
raypath to the subsurface reflection point ![]() , and incorporates the
amplitude effects of source (receiver) directivity, geometric spreading,
transmission loss, and intrinsic high-frequency Q attenuation.
All of these quantities are readily available by raytracing through the
background migration velocity model. The scalar U may be the wave pressure
measured in a hydrophone, the magnitude of the displacement vector measured
at a geophone, or an individual (e.g. vertical) component of the displacement
vector if the appropriate component directivity is introduced into Ar.
, and incorporates the
amplitude effects of source (receiver) directivity, geometric spreading,
transmission loss, and intrinsic high-frequency Q attenuation.
All of these quantities are readily available by raytracing through the
background migration velocity model. The scalar U may be the wave pressure
measured in a hydrophone, the magnitude of the displacement vector measured
at a geophone, or an individual (e.g. vertical) component of the displacement
vector if the appropriate component directivity is introduced into Ar.
It is important to note that the volume integration (2) models a single trace for any arbitrary source and receiver location. There is no ``preferred'' acquisition geometry for this synthesis; it works for shot gathers as well as random trace orientations. In particular, (2) is perfectly adequate for constant offset survey data, which will be the focus of this work.