The choice of integration methods

Double time integration of the data traces is performed before migration and after modeling in subroutine kfastaax() by calling subroutine doubint() . For conj==0 causal integration is followed by anticausal integration and for conj==1 anticausal integration is followed by causal integration. This strategy for creating triangular weighting functions along the operator trajectory by double integration is applied to 3-D migration by Lumley 1993 and to 3-D DMO by Blondel 1993. Theoretical aspects of anti-aliasing and integration along a line are discussed by Nichols 1993.

The main issue of this report is to analyze the difference between using causintold() and causintnew() . In the last report we used causintnew(), but earlier algorithms which perform similar operations with trimo() use causintold() Claerbout (1992).

Causal integration is defined as

$$y(t) = \int_{-\infty}^t x(\tau) d\tau \:.$$

The discrete version of this integral can be represented by the following matrix equation:  

$$\left[ \begin{array} {c} y_0 \\ y_1 \\ y_2 \\ y_3 \\ y... ... x_5 \\ x_6 \\ x_7 \\ x_8 \\ x_9 \\ \end{array} \right]$$ (1)

This is implemented by causintnew() . With 1/2 on the diagonal the summation $\int_{-\infty}^t + \int_t^{\infty} = \int_{-\infty}^{\infty}$is exactly true, so it seems that causintnew() is an improvement over causintold() which has 1 on the diagonal.

In terms of Z-transforms, causintnew() is represented by the bilinear transform  

$$Y(Z) \; = \; {{1}\over {2}} \: {{1 \: + \: Z}\over{1 \: - \: Z}} \; X(Z)\:,$$ (2)

causintold() is represented by  

$$Y(Z) \; = \; {{1}\over{1 \: - \: Z}} \; X(Z)\:.$$ (3)

Both Equations have poles at Z = 1, corresponding to $\omega = 0$.Equation (2) has a zero at Z = -1 which is the Nyquist frequency $\omega = \pi$. The result of putting the zero in the numerator of equation (2) is that causintnew() acts to low-pass filter the input signal more than causintold().

The net effect of modeling with causintnew(), including half-order differentiation can be represented in terms of Z-transform as multiplication by  

$${{-\,(1 \: + \: Z)^2\:\sqrt{(1\: - \: Z)}}\over{4\:(1 \: - \: Z)^2}}\:.$$ (4)

Similarly, modeling with causintold(), can be represented as multiplication by  

$${{-Z\:\sqrt{(1\: - \: Z)}}\over{(1 \: - \: Z)^2}}\:.$$ (5)

Figure 1 illustrates the actions of causintold() and causintnew(). Triangles are created by integrating three spikes causally and then anticausally. The triangle created by double application of causintold() is plotted on the second line of Figure 1. It is sharper and narrower than the triangle created by double application of causintnew and displayed on the third line of Figure 1. The last two lines in Figure 1 are the result of the application of equations (5) and (4). The application of causintnew to implement equation (4) results in a smoother and broader phase shifted triangle.

The effect of using causintnew is to low-pass filter the result which is obtained by using causintold(). This effect is even more evident when the routines are used in conjunction with kfastaax() on synthetic data.

 

caus Figure 1 The first line is the input to the double causal integration subroutine. Second and third lines are triangles created by applying double integration using causintold() and causintnew(). The fourth and fifth lines are the result of applying the half-order differential before double integration. The triangles created with causintold() are narrower and sharper than the ones created with causintnew().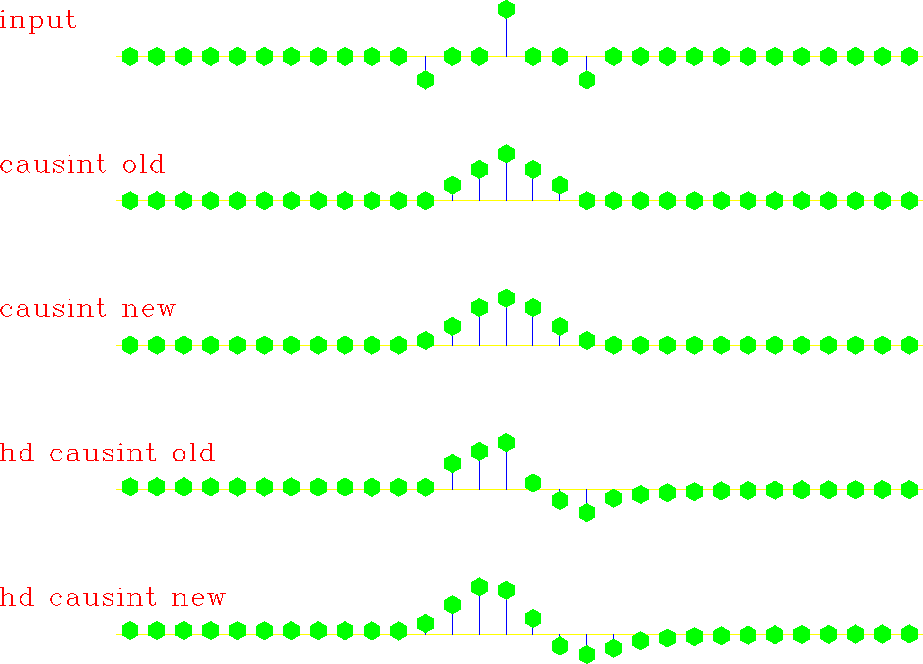