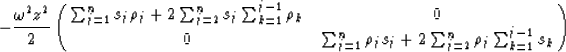Next: Lag formulation
Up: DEVELOPMENT
Previous: Taylor series expansion
Since this translational operator is now in terms of parameters v and
 which are constant across layer boundaries, we can form the
n-layer transformation by forming the product of the n individual
layer transformations. In the case of the first three terms of our
truncated power series approximation of Equation 8,
this leads to
which are constant across layer boundaries, we can form the
n-layer transformation by forming the product of the n individual
layer transformations. In the case of the first three terms of our
truncated power series approximation of Equation 8,
this leads to
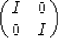
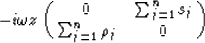
| 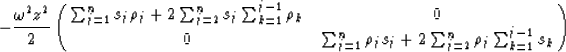 |
(9) |





Next: Lag formulation
Up: DEVELOPMENT
Previous: Taylor series expansion
Stanford Exploration Project
11/17/1997
![]()
![]()