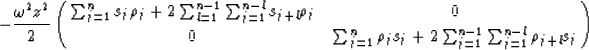Lag formulation

Without changing the outcome, the double summations in Equation 9 can be rewritten in terms of lags (l), and the n-layer transformation operator now looks like:

$$\pmatrix{ I & 0 \cr 0 & I }$$

$$- i \omega z \pmatrix{ 0 & \sum_{j=1}^{n} s_{j} \cr \sum_{j=1}^{n} \rho_{j} & 0 }$$

 

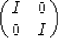
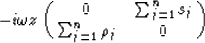
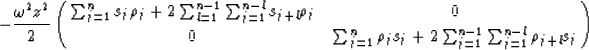$$- \frac{\omega^{2} z^{2}}{2} \pmatrix{ \sum_{j=1}^{n} s_{j... ...s_{j} + 2\sum_{j=1}^{n-1} \sum_{j=1}^{n-l} \rho_{j+l} s_{j} }$$ (10)