A stationarity condition

The anti-symmetric term, 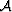${\cal A}$, is a scalar which accounts for linear trends in the addable material constants. 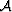${\cal A}$ can be removed from the problem by removing any such trends from 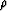$\rho$ and s without altering their sum values. With this, Equation 11 becomes

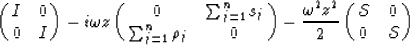$$\pmatrix{ I & 0 \cr 0 & I } - i \omega z \pmatrix{ 0 &... ...ega^{2} z^{2}}{2} \pmatrix{ {\cal S} & 0 \cr 0 & {\cal S} }$$ (12)

 which can be rewritten  

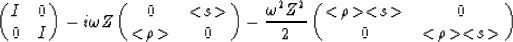$$\pmatrix{ I & 0 \cr 0 & I } - i \omega Z \pmatrix{ 0 &... ...{ <\!\rho\!\gt<\!s\!\gt & 0 \cr 0 & <\!\rho\!\gt<\!s\!\gt }$$ (13)