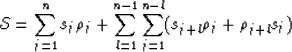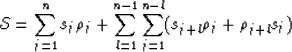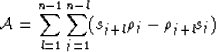Next: A stationarity condition
Up: DEVELOPMENT
Previous: Lag formulation
Now set
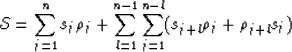
that is, 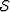 is the sum of products of s and
is the sum of products of s and 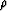 over all
instances and lags, and
over all
instances and lags, and
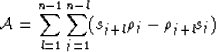
so that 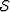 and
and 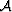 are, respectively, the symmetric and
anti-symmetric components of the principal diagonal of the second-order
matrix. The n-layer transformation of Equation 10 is now
are, respectively, the symmetric and
anti-symmetric components of the principal diagonal of the second-order
matrix. The n-layer transformation of Equation 10 is now
| 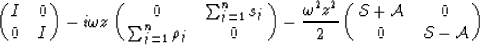 |
(11) |





Next: A stationarity condition
Up: DEVELOPMENT
Previous: Lag formulation
Stanford Exploration Project
11/17/1997