




Next: SPRINGS IN SERIES
Up: Dellinger & Muir: Dix
Previous: Dellinger & Muir: Dix
The Dix equations are usually written in the form
| 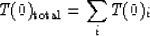 |
(1) |
and
| 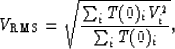 |
(2) |
where T(0)i is the vertical traveltime and
Vi is the moveout velocity for the ith layer,
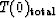 is the total traveltime through
the stack, and
is the total traveltime through
the stack, and 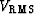 is the near-offset
moveout velocity for the stack.
This form for the equations is favored because it corresponds directly
to surface data measurements.
It is also consistent: the stack as a whole is parameterized in the
same way as the individual layers.
This would not have been the case if we had used, for example,
layer thickness and isotropic velocity;
the vertical velocity for the stack as found from
is the near-offset
moveout velocity for the stack.
This form for the equations is favored because it corresponds directly
to surface data measurements.
It is also consistent: the stack as a whole is parameterized in the
same way as the individual layers.
This would not have been the case if we had used, for example,
layer thickness and isotropic velocity;
the vertical velocity for the stack as found from
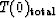 is not generally the same as the near-offset moveout velocity
is not generally the same as the near-offset moveout velocity
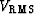 ,so an isotropic parameterization for the stack as a whole is not possible.
,so an isotropic parameterization for the stack as a whole is not possible.
The usual method of deriving equations (1) and (2)
involves finding a power series for the stack traveltime
in the form
| 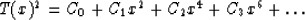 |
(3) |
and comparing this stack equation with
the corresponding one for a single layer,
| 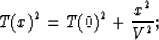 |
(4) |
see for example section 4.1 in Hubral and Krey (1980).
This method is not particularly well suited
to the task of finding anisotropic extensions
of the Dix equations.
The algebra involved is tedious even for the isotropic case,
and a general expression for the Ci in equation (3)
provides more information than we need.
We propose instead a direct method that makes use of key
concepts from the Schoenberg-Muir calculus (Schoenberg and Muir, 1989).
Although the Dix equations and the Schoenberg-Muir calculus may appear
to be unrelated, both are equivalent-medium theories;
both show how to replace a stack of layers with a bulk
homogeneous equivalent that is (in some sense) indistinguishable from
the heterogeneous stack.
The concepts underlying the Schoenberg-Muir derivation apply equally well
to rays in layered media
and provide a framework for an alternative derivation of the Dix equations
more amenable to anisotropic extension.
We begin with the canonical problem of the type, ``springs in series''.
We then show how the same concepts apply to the Schoenberg-Muir calculus,
and finally recast Dix's model of paraxial rays in layered media.





Next: SPRINGS IN SERIES
Up: Dellinger & Muir: Dix
Previous: Dellinger & Muir: Dix
Stanford Exploration Project
11/17/1997