




Next: About this document ...
Up: Palacharla: Filter design
Previous: ACKNOWLEDGEMENTS
- Biondi, B., and Palacharla, G., 1993, 3-D wavefield depth extrapolation by rotated McClellan filters: SEP-77, 27-36.
-
- Hale, D., 1991, 3-D depth migration via McClellan transformations: Geophysics, 56, 1778-1785.
-
- Lu, W.-S., and Antoniou, A., 1992, Two-dimensional digital filters: Marcel Dekker Inc.
-
- McClellan, J., and Chan, D., 1977, A 2-D FIR filter structure derived from the Chebyshev recursion: IEEE Trans. Circuits Syst., CAS-24, 372-384.
-
- Nautiyal, A., Gray, S. H., Whitmore, N. D., and Garing, J. D., 1993, Stability versus accuracy for an explicit wavefield extrapolation operator: Geophysics, 58, 277-283.
-
- Parks, T., and Burrus, C., 1987, Digital filter design: John Wiley and Sons.
-
- Soubaras, R., 1992, Explicit 3-D migration using equiripple polynomial expansion and Laplacian synthesis: 62nd Ann. Internat. Mtg., Soc. Explor. Geophys., Expanded Abstracts, 905-908.
-
APPENDIX A
In this Appendix, I give the Chebyshev recursion formula and
the different approximations to
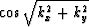 .
The Chebyshev recursion formula is given by,
.
The Chebyshev recursion formula is given by,
| ![\begin{displaymath}
\cos{nk} = 2\cos{\left[(n-2)k \right ]}\cos{k} - \cos{\left [(n-1)k \right ]}\end{displaymath}](img26.gif) |
(9) |
The original McClellan transformation is given by
| 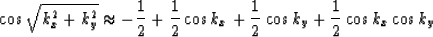 |
(10) |
The modified McClellan transformation is given by (taken from Hale (1991)),
| 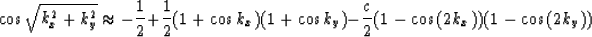 |
(11) |
where c is chosen, by exactly matching a particular value k along the
diagonal kx=ky. c=0.0255 was used here, which corresponds to k=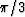 .
.
The 2-D filter in the x-y domain corresponding to the original
McClellan transformation is given by,
| 1/8 |
1/4 |
1/8 |
| 1/4 |
-1/2 |
1/4 |
| 1/8 |
1/4 |
1/8 |
The 2-D filter in the x-y domain corresponding to the modified McClellan
transformation is given by (taken from Hale (1991)),
| -c/8 |
0 |
c/4 |
0 |
-c/8 |
| |
1/8 |
1/4 |
1/8 |
|
| c/4 |
1/4 |
-(1+c)/2 |
1/4 |
c/4 |
| |
1/8 |
1/4 |
1/8 |
|
| -c/8 |
|
c/4 |
|
-c/8 |
The 2-D filters have a quadrantal symmetry, so the number of floating
point operations required for the 2-D convolution of the filter with
data is reduced.





Next: About this document ...
Up: Palacharla: Filter design
Previous: ACKNOWLEDGEMENTS
Stanford Exploration Project
11/17/1997
![]() .
The Chebyshev recursion formula is given by,
.
The Chebyshev recursion formula is given by,