




Next: HANKEL TAIL
Up: Claerbout: Hankel tail
Previous: INTRODUCTION
Causal integration
is represented in the time domain
by convolution with a step function.
In the frequency domain this amounts to multiplication by 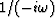 .Integrating twice amounts to convolution by a ramp function,
.Integrating twice amounts to convolution by a ramp function,
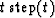 , which in the Fourier domain is multiplication by
, which in the Fourier domain is multiplication by
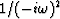 .Integrating a third time is convolution with
.Integrating a third time is convolution with
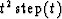 which in the Fourier domain is multiplication by
which in the Fourier domain is multiplication by
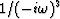 .In general
.In general
| 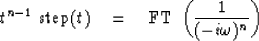 |
(1) |
Proof of the validity of equation (1) for integer values of n
is by repeated indefinite integration which also indicates
the need of an n! scaling factor.
Proof of the validity of equation (1) for fractional values of n
would take us far afield mathematically.
(Fractional values of n, however,
are exactly what we need to interpret Huygen's secondary wave sources in 2-D.)
The factorial function of n in the scaling factor becomes a gamma function.
The poles suggest that a more thorough mathematical study of convergence
is warranted, but this is not the place for it.
A common application is when n=1/2 and
(ignoring the scale factor)
equation (1) becomes
| 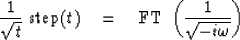 |
(2) |
It is well known that
| 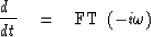 |
(3) |
A product in the frequency domain corresponds
to a convolution in the time domain.
A time derivative is like convolution with a doublet 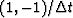 .Thus, from
equation (2) and
equation (3)
we obtain
.Thus, from
equation (2) and
equation (3)
we obtain
| 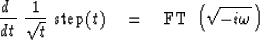 |
(4) |





Next: HANKEL TAIL
Up: Claerbout: Hankel tail
Previous: INTRODUCTION
Stanford Exploration Project
11/17/1997
![]() .Integrating twice amounts to convolution by a ramp function,
.Integrating twice amounts to convolution by a ramp function,
![]() , which in the Fourier domain is multiplication by
, which in the Fourier domain is multiplication by
![]() .Integrating a third time is convolution with
.Integrating a third time is convolution with
![]() which in the Fourier domain is multiplication by
which in the Fourier domain is multiplication by
![]() .In general
.In general