Forward modeling operator

To do forward modeling for a poststack section, we need only consider the locations of geophones. However, in the prestack case, we need to consider the location of both the shots and the geophones, because upward extrapolation using the DSR equation requires both shot and geophone continuation. Thus the spatial filter that stops and keeps extrapolating the wavefield according to the geophone and shot locations becomes more complicated than the filter used in poststack datuming.

The prestack forward modeling can be formulated by propagating the wavefield upward with a filter between extrapolation steps to stop the wavefield propagation after recording for the geophone continuation and after reaching the depth level of each shot for shot continuation. In addition to the filter to stop the wavefield, we need one more operator to save some wavefields that have reached either a shot or a geophone but not the other, for further extrapolation in the corresponding space. Then at all depth levels all wavefields that have reached both a geophone and a shot are summed to produce the prestack wavefield along the irregular surface. In order to explain the algorithm clearly and schematically, I use a simple geometry that has only two geophones and two shots on an irregular surface, as illustrated in Figure 12.

 

synpretopo Figure 12 Synthetic surface recording geometry for prestack data. S and G represent the shot and geophone axes, respectively. Z represents depth.

Figure 13 is a schematic diagram of the forward modeling algorithm, in which W_s,i and W_g,i represent upward extrapolation at the i-th depth level for the common-geophone gathers (CGG) and common-shot gathers (CSG), respectively. K_g/s,i, H_g/s,i, and F_g/s,i are spatial filters for stopping, passing, and grabbing the wavefield at the i-th depth level according to the geophone and shot locations, respectively. Each small rectangle in Figure 13 represents an abstract vector that contains wavefields at the corresponding spatial location.

 

tppremdl
Figure 13 Prestack forward modeling scheme: the schematic diagram for prestack forward modeling when the surface is given by Figure 12. W_s,i and W_g,i represent upward extrapolation for the common-geophone gathers (CGG) and the common-shot gathers (CSG), respectively, at the i-th depth level. K_g/s,i, H_g/s,i, and F_g/s,i are spatial filters. The solid and empty rectangles in the filter numerically represent 1 and , respectively.

The forward scheme shown in Figure 13 can be algebraically generalized, if we divide the topography into z levels, as follows:

$$\left[ \begin{array} {c} d_0 \end{array} \right] = \left[ \b... ...array} \right] \left[ \begin{array} {c} d_z \end{array} \right]$$ (7)

$$E_{s,i} = \left[ \begin{array} {ccc} I&0&0\\ 0&I&0\\ 0&0&W_{s,i}\\ \end{array} \right]$$ (8)

$$G_{s,i} = \left[ \begin{array} {ccc} I&0&H_{g,i-1}F_{s,i}\\ ... ...K_{s,i}\\ 0&I&K_{g,i-1}(F_{s,i}+K_{s,i})\\ \end{array} \right]$$ (9)

$$G_{g,i} = \left[ \begin{array} {ccc} I&0&H_{s,i}F_{g,i}\\ 0... ...i}K_{g,i}\\ 0&I&K_{s,i}(F_{g,i}+K_{g,i})\\ \end{array} \right]$$ (10)

where

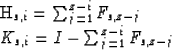In equation (7), d₀ and d_z are wavefields on the irregular surface and the datum level, respectively. The shot extrapolation operator E_s and the geophone extrapolation operator E_g are followed by the shot spatial filter G_s and the geophone spatial filter G_g, respectively, at every depth level. For example, the function of the operator G_s is to sort wavefields into three groups:

• Wavefields that have reached the surface in the shot space among wavefields that have reached the surface in the geophone space. This work is done by the first row of G_s, and the wavefields are saved for the final output.
• Wavefields that have not reached the surface in the shot space among wavefields that have reached the surface in the geophone space. This work is done by the second row of G_s, and the wavefields are saved to be used for the shot extrapolation at the next depth level.
• Wavefields that have not reached the surface in any space. This work is done by the third row of G_s, and the wavefields are saved to be used for the geophone extrapolation use at the same depth level.

The operator G_g works similarly to G_S.