THE TRIANGLE AS AN ANTI-ALIASING STRUCTURE

In the Fourier domain, the operator is not aliased. However, integral methods must be applied carefully to account for operator aliasing.

For a given temporal frequency of the data, the increase in the dip of the operator produces an increase in the spatial frequency until it reaches the Nyquist frequency (two points per wavelength). Beyond that point, the operator is aliased.

Claerbout 1992 introduced an efficient technique to avoid the aliasing of the operator with Kirchhoff methods. Instead of spreading a simple spike along the operator, a dip-dependent triangle is effectively convolved with the operator. Assuming spatial spacing of $\Delta x$, the width of the triangle at a point of the operator is determined by equation (2)  

$$\Delta_t = \left( \frac{dt_0}{dx} \right) \Delta x ,$$ (2)

where $\left( \frac{dt_0}{dx} \right)$ is the operator dip. It is therefore assured that the operator always has at least two points per wavelength on the spatial axis, even when the time frequency of the data is Nyquist.

Figure (2) shows the impulse response of a spike when the triangle anti-aliasing method is used. The phase shift caused by the half differential filter (usual in Kirchhoff methods) makes the triangles look like the teeth in a shark's jaw.

 

Iraa Figure 2 Impulse response of the anti-aliasing integral DMO using triangles. Input spike: 1.0 s; velocity: 2000 ms-1.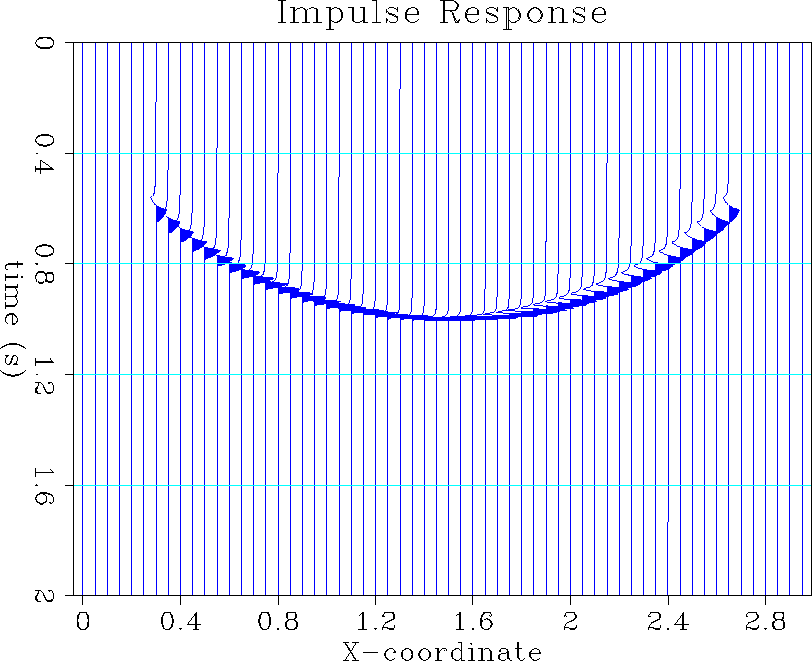

The triangular weight can be built with three spikes $(-\frac{\Delta_t}{2},\ldots,\Delta_t,\ldots,-\frac{\Delta_t}{2})$submitted to both causal and anticausal integration. The anti-aliasing process is cheap because each output trace is double integrated only once.