




Next: The effect of the
Up: AMPLITUDES ALONG THE DMO
Previous: Different weighting schemes
As suggested by the preceding result, spherical divergence
should be included in the DMO process. Indeed, for a given
shot-geophone traveltime, the zero-offset ray path when the
reflector is dipping is shorter than when the reflector is
horizontal. Since the decrease in amplitude of a spherical
wave is inversely proportional to the distance traveled,
the spherical spreading is clearly related to the dip of the
structures and, thus, must be included in the DMO process.
Gardner 1990 expressed the spherical
spreading factor as a function of k (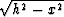 ) and
t2 (t0). As a function of h, tn, and x, it becomes
) and
t2 (t0). As a function of h, tn, and x, it becomes
| 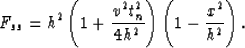 |
(6) |
The two first terms of expression (6) account for the
offset and the depth of the reflector, whereas the third
term clearly accounts for its dip.





Next: The effect of the
Up: AMPLITUDES ALONG THE DMO
Previous: Different weighting schemes
Stanford Exploration Project
11/17/1997
![]() ) and
t2 (t0). As a function of h, tn, and x, it becomes
) and
t2 (t0). As a function of h, tn, and x, it becomes