




Next: CONCLUSION
Up: P-VELOCITIES FOR DIFFERENT FREQUENCIES
Previous: The low frequency-high frequency
Fig2.7
Figure 9 Calculated velocity versus
frequency for sand, silt, and clay. For a sand of 40% porosity and
10 Darcy permeability, critical frequency is in the sonic-ultrasonic
range (10-100 kHz). For a silt of 60% porosity and 10 mD permeability,
critical frequency is in the high ultrasonic frequency range (10 MHz).
In clay with 80% porosity and permeability of the order of 0.5 mD,
critical frequency is in the GHz range. Figure and caption taken from Marion
1990, Figure 2.7.

Figure (9) displays some theoretical
velocity-frequency curves for different
materials (sand, silt, and clay). The shape of these curves
is sigmoid: the velocity is constant for low frequencies
until it reaches a transitional region where it strongly increases
to reach eventually another constant-velocity level
corresponding to the high frequencies. As explained in the section on
diffracted waves, using diffraction theory we can predict the low and high
levels of velocity for low and high frequencies. Moreover,
in the preceding section we arrived at a condition that locates
the limit between low frequencies and high frequencies. If we
apply this condition to the three curves by picking the frequency at
which the sigmoid pattern occurs, we can estimate
the radius of the grains. For the clay, the estimate
of the radius is 0.1 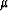 m. The silt and the sand
give us approximately 10
m. The silt and the sand
give us approximately 10 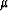 m and 2 mm, respectively.
The silt and clay samples can be considered as suspensions
because of their high porosity (60% and 80%). Therefore, the
estimation of the grain size gives some realistic results.
Unfortunately, since the sand with 40 percent porosity cannot be
considered a suspension, condition (8) is no longer valid.
However, the condition gives interesting predictions of
the grain size.
m and 2 mm, respectively.
The silt and clay samples can be considered as suspensions
because of their high porosity (60% and 80%). Therefore, the
estimation of the grain size gives some realistic results.
Unfortunately, since the sand with 40 percent porosity cannot be
considered a suspension, condition (8) is no longer valid.
However, the condition gives interesting predictions of
the grain size.





Next: CONCLUSION
Up: P-VELOCITIES FOR DIFFERENT FREQUENCIES
Previous: The low frequency-high frequency
Stanford Exploration Project
11/17/1997
