SYNTHETIC EXAMPLE

P- and SV-wave synthetic traveltimes were generated using the anisotropic ray tracing algorithm described in Michelena (1992b). Figure  shows the heterogeneous TI model where the rays were traced. This model shows the variation in depth of $V_{ij} = \sqrt{c_{ij}/\rho}$,the elastic constants transformed to velocity assuming unit density. The cross-well geometry used to compute the traveltimes consists of 92 sources and 92 receivers at each well. The distance between wells is 390 feet, and the separations between consecutive sources or receivers is 23 feet.

 

elastic-exacto Figure 1 Layered TI synthetic model. From left to right the four curves represent the elastic constants in units of velocity V44, V13, V33, and V11, respectively. The density is assumed to be unity.

Since the elastic constants of the medium are known, the corresponding elliptical velocities (V_P,x, $V_{P,z{\rm NMO}}$, V_SV,x, and $V_{SV,z{\rm NMO}}$) can be calculated easily by using the equations derived in Michelena (1992c). Figure  shows the result. These velocities can be used to check how the algorithm performs in the first step toward the estimation of the elastic constants, that is, the tomographic estimation of the elliptical velocities.

The paraxial elliptical approximation around the horizontal axis (assuming vertical axis of symmetry) is accurate for angles of less than 30 degrees (Michelena, 1992c). For this reason, the inversion only uses rays whose angle measured from the horizontal satisfies this condition. However, no approximation is made in the computation of the synthetic traveltimes through the model of Figure . The paraxial approximation is made only during the inversion procedure in which the rays are traced in elliptically anisotropic instead of transversely isotropic models.

The fact that the straight line that connects a source-receiver pair forms a small angle with respect to the horizontal doesn't necessarily mean that the angle of the corresponding ray path is also small. The angle of the ray path increases in low-velocity layers and

 

syn-ellip Figure 2 Theoretical elliptical velocities around the horizontal axis calculated from the elastic constants shown in Figure 1. From left to right the four curves represent VSV,x, $V_{SV,z{\rm NMO}}$, $V_{P,z{\rm NMO}}$, and VP,x, respectively.

decreases in high-velocity layers. However, if the velocity contrasts are not too strong, it should be enough to look at the straight line that connects source and receiver to select the rays that satisfy the proper constraints.

Figure  shows the result of inverting the P-wave traveltimes. This figure also shows the theoretical elliptical velocities calculated from the elastic constants. The estimation of the horizontal P-wave velocity is, as expected, almost perfect, whereas the vertical NMO velocity is slightly overestimated ($\approx 3\%$) in all layers. As Figure  shows, the estimation of the vertical NMO velocity is more accurate when inverting SV-wave traveltimes than when inverting P-wave traveltimes, which means that, for the range of ray angles used, the elliptical approximation works better for SV-waves than for P-waves. The error in $V_{SV,z{\rm NMO}}$ is less than one percent.

The errors in the NMO velocities $V_{P,z{\rm NMO}}$ and $V_{SV,z{\rm NMO}}$come from using an elliptical approximation for ray angles that are not sufficiently small. When the model is truly elliptical, the estimation of the NMO velocities is accurate.

 

syn-ellip-p Figure 3 P-wave elliptical velocities. Dashed lines: result of the inversion of P-wave traveltimes with a ray angle of less than 30 degrees. Continuous lines: theoretical values. The curves with lower velocity correspond to $V_{P,z{\rm NMO}}$, and the ones with higher velocity correspond to VP,x.

 

syn-ellip-s Figure 4 SV-wave elliptical velocities. Dashed lines: result of the inversion of SV-wave traveltimes with a ray angle of less than 30 degrees. Continuous lines: theoretical values. The curves with lower velocity correspond to VSV,x, and the ones with higher velocity correspond to $V_{SV,z{\rm NMO}}$.

The variation with depth in the theoretical P- and SV-wave elliptical velocities has been estimated accurately. Therefore, by using these two models of elliptical velocities, we can also expect an accurate estimation of the elastic constants, as Figure  shows.

Since P- and SV-wave traveltimes are inverted separately and the interfaces are not constrained to move consistently with both data sets, the models obtained for P- and SV-wave elliptical velocities may not have all the interfaces at exactly the same depths. As a consequence, artificial thin layers (spikes) may appear when we estimate the elastic constants because there may be slight relative mispositions of the same boundaries in the two models. In Figure  these spikes are removed by applying a median filter to the elastic constants after the mapping from elliptical velocities. Another way to solve this problem is by describing the interfaces with the same parameters for both P- and SV-wave velocity models and inverting the two sets of traveltimes simultaneously.

Depending on the radiation pattern of the source, traveltimes that correspond to nearly horizontal rays may not always be available for either P- or SV-waves. When this happens, it may be necessary to use ray angles that are far from the horizontal because nothing else is available. Figure  shows an example where SV-wave elliptical velocities have been estimated by using ray angles between 28 and 36 degrees. The estimated horizontal component of the velocity is as accurate as in Figure  even though this component is not well sampled by the ray paths used. The error in $V_{SV,z{\rm NMO}}$ increases when using larger ray angles. However, as Figure  indicates, the error in the estimation of the elastic constants is still small because the P-wave elliptical velocities were estimated using small ray angles.

 

exact-vs-approx-median Figure 5 Elastic constants that control P- and SV-wave propagation. Dashed lines: estimated. Continuous lines: given. From left to right the four pairs of curves represent V44, V13, V33, and V11, respectively.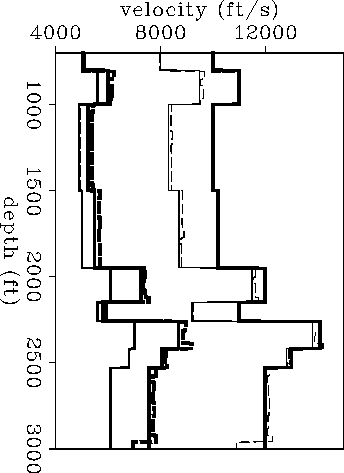

 

syn-ellip-s-28to36 Figure 6 SV-wave elliptical velocities. Dashed lines: result of the inversion of SV-wave traveltimes with ray angles between 28 and 36 degrees. Continuous lines: theoretical SV-wave elliptical velocities. The curves with lower velocity correspond to VSV,x and the ones with higher velocity correspond to 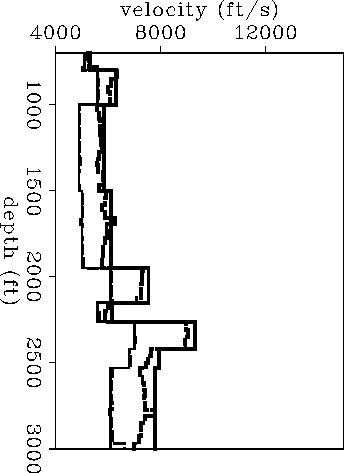$V_{SV,z{\rm NMO}}$.

 

exact-vs-approx-28to36 Figure 7 Elastic constants that control P- and SV-wave propagation. Dashed lines: elastic constants estimated when the ray angles used in the tomographic inversion of SV-wave traveltimes are between 28 and 36 degrees. The ray angles used to obtain the P-wave elliptical velocities are between 0 and 30 degrees, as in Figure 5. Continuous lines: original elastic constants. From left to right the four pairs of curves represent V44, V13, V33, and V11, respectively.

In the field data example that follows, SV-wave traveltimes are not available for small vertical offsets.