




Next: USING 3-D EIKONAL EQUATION
Up: Berlioux: 3-D Eikonal equation
Previous: INTRODUCTION
In two dimensions, considering one-way time, the wave equation is
| 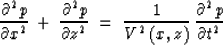 |
(1) |
where 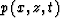 is the pressure wave field, and
is the pressure wave field, and 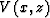 is the
velocity of the wave propagation in the medium.
is the
velocity of the wave propagation in the medium.
We can make the following approximation of the wave field:
| 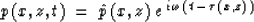 |
(2) |
expressing the pressure wave field in term of amplitude 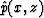 and
phase
and
phase 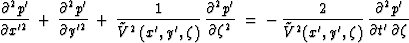 , where
, where  is the
traveltime along the ray paths. Then replacing (2) in equation
(1) and making the high frequency approximation, we obtain the 2-D
Eikonal equation:
is the
traveltime along the ray paths. Then replacing (2) in equation
(1) and making the high frequency approximation, we obtain the 2-D
Eikonal equation:
| 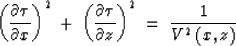 |
(3) |
Among other uses, this equation is useful to compute traveltimes of rays
in a given earth model.
V.J. Khare introduced the following equation for the ray-theoretic
interpretation of all-angle time migration Khare (1991):
| 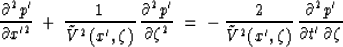 |
(4) |
where 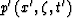 and
and 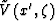 are respectively the
pressure wave field and the wave propagation velocity in the time-retarded
coordinate system Claerbout (1976),
are respectively the
pressure wave field and the wave propagation velocity in the time-retarded
coordinate system Claerbout (1976),
| 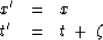 |
(5) |
with the time-like vertical coordinate 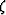 Lowenthal et al. (1985),
Lowenthal et al. (1985),
| 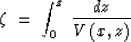 |
(6) |
If we make the following approximation of the wave field in the new coordinate
system, equivalent to the equation (2):
| 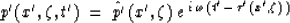 |
(7) |
we can express the 2-D Eikonal equation for time migration giving the
traveltime 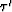 in the frequency domain in the time-retarded coordinate
system:
in the frequency domain in the time-retarded coordinate
system:
| 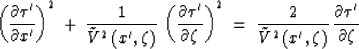 |
(8) |
Using equations (5) and (6), we obtain the 2-D Eikonal
equation for time migration in the physical coordinate system:
| 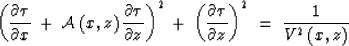 |
(9) |
with
| 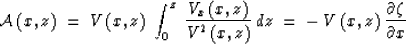 |
(10) |





Next: USING 3-D EIKONAL EQUATION
Up: Berlioux: 3-D Eikonal equation
Previous: INTRODUCTION
Stanford Exploration Project
11/17/1997