Downward continuation

Ultimately, I would like to input an initial image from this slant stack result into a downward continuation program as a first guess at the velocity structure. This first guess could then be refined using an iterative method. The criteria for when a satisfactory velocity has been converged upon could then be the elimination of the ``X'' patterns and/or hyperbolic trajectories in shot or offset space. Both these criteria are essentially the same and will be satisfied when an adequate velocity is converged upon.

 

syndn
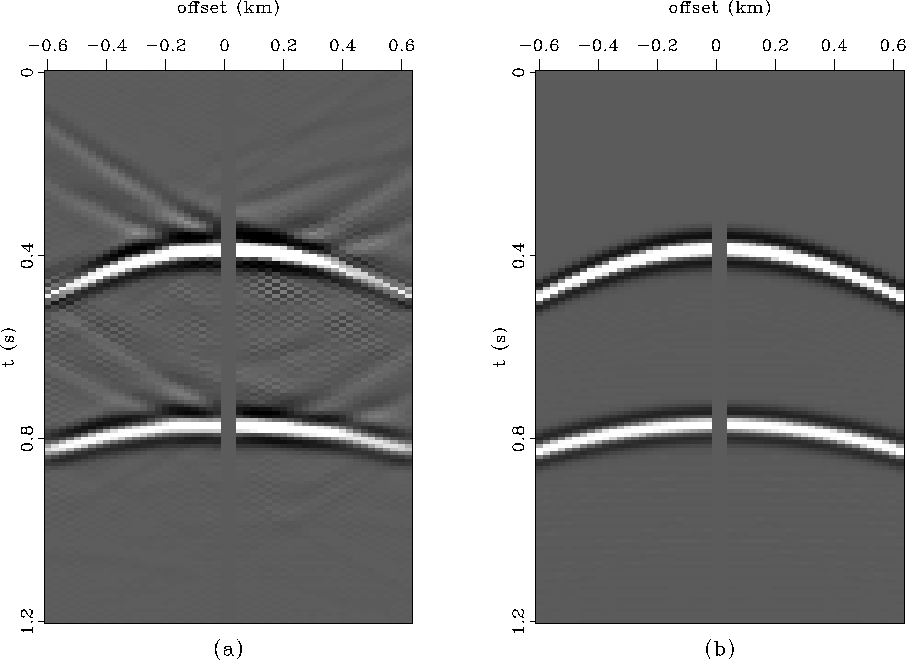
Figure 6 Comparison of (a) a synthetic shot gather downward continued through the velocity perturbation with the exact velocity model and (b) the original synthetic data.

At the time of this writing, I am not ready to input the result of the slant stack code into the downward continuation code; However, I can demonstrate how the distortions due to the velocity perturbation can be removed. In Figure 6a I have taken the data from Figures 2b and  3 and downward continued through the exact velocity model. The effect of the velocity perturbation is removed. The kinematics are restored but some artifacts and amplitude effects remain. This downward continuation is performed using the Kirchhoff code discussed earlier. In order to parameterize velocity it will be more convenient to perform the wavefield extrapolation by using a finite-difference code or by calculating finite-difference traveltimes for the Kirchhoff scheme.