IMPROVED McCLELLAN FILTERS

The McClellan filters proposed by Hale 1991 to approximate the $\cos\mid\vec k\mid$ filter have the important advantage of being compact, and thus inexpensive to apply as convolutions in the space domain. The lower-order filter is applied by convolving the data with a nine-point stencil, the higher-order one by convolving the data with a 17-point stencil. However, both filters have an anisotropic impulse response, that is, their spectra vary with azimuth. Our last report Biondi and Palacharla (1993) suggested an improvement to the impulse response of the McClellan filter. The improved filter has less dispersion than either of the McClellan filters, and has a computational cost comparable to that of the 17-point filter. The new filter was obtained by averaging the 9-point McClellan filter with a 45 degree rotated version of it.

In this section we suggest a further improvement on the circular response of the McClellan filter. The representation of the 9-point McClellan filter in the wavenumber domain is:  

$$\cos\sqrt{k_x^2 + k_y^2}\approx MC_0\left(k_x,k_y\right)=-1+{1\over{2}}\left(1+\cos k_x\right)\left(1+\cos k_y\right).$$ (2)

The modified McClellan transformation is given by the following equation from Hale 1991:  

$$\cos{\sqrt{k_x^2 + k_y^2}} \approx -\frac{1}{2} + \frac{1}{2... ...(1+\cos{k_y})} - \frac{c}{2}{(1- \cos{(2k_x)})(1-\cos{(2k_y)})}$$ (3)

where c is chosen by exactly matching a particular value k along the diagonal k_x=k_y. The value c=0.0255 was used here, which corresponds to k=$\pi/3$.

Rotating the 9-point filter by an azimuth of 45 degrees and scaling the axes to match the original filter along the axes leads to the expression Biondi and Palacharla (1993):  

$$\overline{{MC}_{45}}\left(\overline{k_x},\overline{k_y}\righ... ...ht)+ \cos\left({\overline{k_y}\over{2}}\right)-1 \right] }^{2}.$$ (4)

 

all
Figure 1 Contours of constant amplitude and phase for the 17-point McClellan transformation filter (double-dashed line), the 9-9 averaged filter (dot-dashed line), the 17-9 averaged filter (dashed line), and the ideal circularly symmetric filter (solid line).

The filter $\overline{{MC}_{45}}\left(\overline{k_x},\overline{k_y}\right)$, as in equation (4) can be efficiently applied to the data because the operator ${\left[ \cos\left({k_x/2}\right)+ \cos\left({k_y/2}\right)-1 \right) }]$ is separable along x and y, its space-domain representation being a cross-shaped convolutional operator. The arms of the cross are the space-domain representation of the cos(k/2) operator. In the last report, we got a more circular response by averaging (2), which represents the original nine-point filter with Equation (4) which represents the rotated 9-point filter. We call this filter the 9-9 averaged filter. Following similar reasoning as that leading to the nine-point averaged filter, the obvious thing to do would be to rotate the 17-point filter by 45 degrees azimuth and then average it with the original 17-point filter, after rescaling the axes such that the rotated 17-point filter matches the original one along the axes. However, it turns out that the remapping of the rotated 17-point filter leads to a fourth- degree equation, which is not simple to solve. Here we suggest, to average the 17-point McClellan filter as given by Equation (3) with the rotated 9-point filter as in Equation (4). We call this filter the 17-9 averaged filter. This new filter gives a more accurate result than the 9-9 averaged filter.

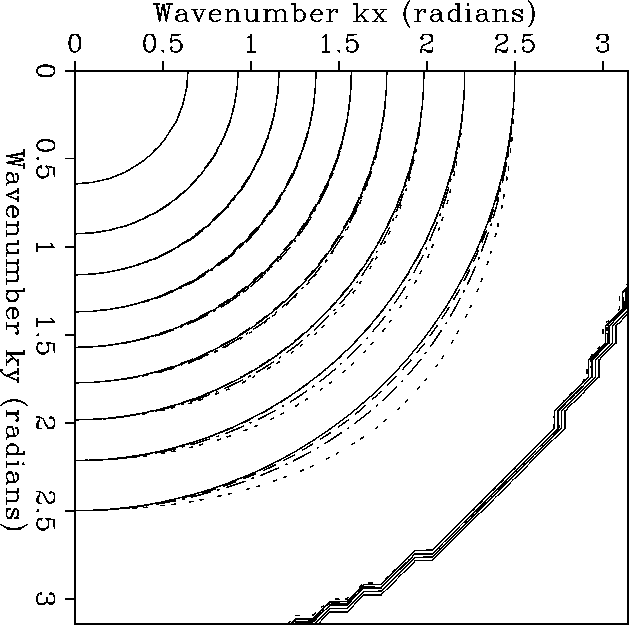
Figure 1 compares the spectrum of the 9-9 averaged filter (the dot-dashed line) with the ideal filter (the solid line) , the 17-point McClellan filter (the double-dashed line), and the 17-9 averaged filter(the dashed line). The spectra of the averaged filters are similar. Both exactly match the ideal spectrum along the axis and deviate from it considerably less than the spectrum of the 17-point McClellan filter across the whole range of azimuths. However, the 17-9 averaged filter gives the closest response to the ideal one. This filter could be realized in a similar way as the 9-9 averaged filter. By alternating the 17-point filter with the rotated 9-point filter on alternate depth steps.